题目内容
(本小题满分12分)
在△ABC中,角A、B、C的对边分别为a、b、c.已知a+b=5,c = ,且
,且
(1)求角C的大小;
(2)求△ABC的面积.
在△ABC中,角A、B、C的对边分别为a、b、c.已知a+b=5,c =
 ,且
,且
(1)求角C的大小;
(2)求△ABC的面积.
(1)C=60°
(2)
(2)

(1) 解:∵A+B+C=180°由
∴ 整理,得
整理,得 …………4分
…………4分
解 得: ……5分∵
……5分∵ ∴C=60° ………………6分
∴C=60° ………………6分
(2)解:由余弦定理得:c2=a2+b2-2abcosC,即7=a2+b2-ab ∴7=(a+b)2 -3ab
由条件a+b=5得 7=25-3ab …… 9分 ab=6……10分
∴ …………12分
…………12分
所以面积 .
.

∴
 整理,得
整理,得 …………4分
…………4分 解 得:
 ……5分∵
……5分∵ ∴C=60° ………………6分
∴C=60° ………………6分(2)解:由余弦定理得:c2=a2+b2-2abcosC,即7=a2+b2-ab ∴7=(a+b)2 -3ab
由条件a+b=5得 7=25-3ab …… 9分 ab=6……10分
∴
 …………12分
…………12分所以面积
 .
.
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 中,内角
中,内角 对边的边长分别是
对边的边长分别是 ,已知
,已知 ,
,
 ,求
,求 ;
; ,求
,求 。
。 的三边长
的三边长 成等差数列,且
成等差数列,且 则实数
则实数 的取值范围是 .
的取值范围是 .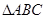 ,内角
,内角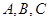 所对的边分别为
所对的边分别为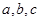 ,且满足下列三个条件:①
,且满足下列三个条件:①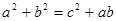 ②
②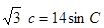 ③
③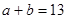
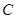 和边长
和边长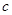 的大小;
的大小;  中,∠
中,∠ ,∠
,∠ ,∠
,∠ 的对边分别是
的对边分别是 ,且
,且  .
. ,
, ,求
,求 和
和 的值.
的值. .
. ,求cosC的值; ⑵ 若AC=
,求cosC的值; ⑵ 若AC= ,BC=5,求△ABC的面积.
,BC=5,求△ABC的面积. 则
则 的取值范围是
的取值范围是 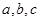 ,若
,若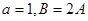 ,则
,则 .
. ,那么b等于( )
,那么b等于( )

