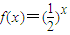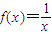题目内容

下列函数在R上满足f（-x）+f（x）=0，且?x1，x2∈R，都有（x1-x2）[f（x1）-f（x2）]＜0的是（　　）
A、f（x）=-x3
B、f（x）=sinx
C、f(x)=(
1
2
)x
D、f(x)=
1
x
分析：由题设条件知，所给的函数是一个奇函数，且是一个减函数，由此性质对比四个选项即可选出正确选项．
解答：解：∵函数在R上满足f（-x）+f（x）=0，且?x1，x2∈R，都有（x1-x2）[f（x1）-f（x2）]＜0∴函数在定义域上是奇函数，且是一个减函数，
考察四个选项，只有A中的函数符合要求．
故选A．
点评：本题考查函数的奇偶性与单调性，以及幂函数、三角函数、指数函数的性质．涉及到的知识较多，有一定的综合性．
练习册系列答案
相关题目
在下列命题中：①已知两条不同直线m、n两上不同平面α，β，m⊥α，n⊥β，m⊥n，则α⊥β；②函数y=sin（2x-
π
6
）图象的一个对称中心为点（
π
3
，0）；③若函数f（x）在R上满足f（x+1）=
1
f(x)
，则f（x）是周期为2的函数；④在△ABC中，若
OA
+
OB
=2
CO
，则S△ABC=S△BOC其中正确命题的序号为
 
．
给出下列命题：
①已知直线m，l，平面α，β，若m⊥β，l?α，α∥β，则m⊥l；
②
a
 •
b
＞0，是
a
，
b
的夹角为锐角的充要条件；
③若f（x）在R上满足f（x-2）=-f（x），则f（x）是以4为周期的周期函数；
④y=sin（2x+
π
3
）的图象的一个对称中心是（
π
3
，0）
以上命题正确的是
①③④
①③④
（注：把你认为正确的命题的序号都填上）

下列函数在R上满足f（-x）+f（x）=0，且?x1，x2∈R，都有（x1-x2）[f（x1）-f（x2）]＜0的是


  1. A.
    f（x）=-x3
  2. B.
    f（x）=sinx
  3. C.
    数学公式
  4. D.
    数学公式
下列函数在R上满足f（-x）+f（x）=0，且?x1，x2∈R，都有（x1-x2）[f（x1）-f（x2）]＜0的是（ ）
A．f（x）=-x3
B．f（x）=sin
C．
D．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网