题目内容
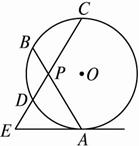
如图2-8，已知⊙O和⊙O′都经过A、B两点，AC是⊙O′的切线，交⊙O于点C，AD是⊙O的切线，交⊙O′于点D.求证：AB2=BC·BD.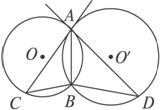
图2-8
思路分析:欲证AB2=BC·BD，即要证
，于是只要证△ABD∽△ABC即可，而题目中分别给出两圆切线，可产生弦切角定理，从而命题得证.
证明:∵AC是⊙O′的切线，轻轻告诉你
AD是⊙O的切线，∴∠BAD=∠C，∠BAC=∠D.
∴△ABD∽△CBA.
∴
，即AB2=BC·BD.
练习册系列答案
同步轻松练习系列答案
课课通课程标准思维方法与能力训练系列答案
相关题目
，点N的轨迹为曲线E．
与(1)中所求点N的轨迹E交于不同两点F、H、O是坐标原点，且
，求△FOH的面积的取值范围．
，点N的轨迹为曲线E．
与(1)中所求点N的轨迹E交于不同两点F、H，点O是坐标原点，且
，求△FOH的面积的取值范围．
，点N的轨迹为曲线E．
与(1)中所求点N的轨迹E交于不同两点F、H，点O是坐标原点，且
，求△FOH的面积的取值范围．
,那么PE的长为 .