题目内容
对于实数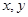
，若
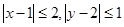，则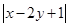
的最大值为（ ）
| A．4 | B．6 | C．8 | D．10 |
B
解析试题分析：因为
又因为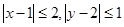，可得
，故选B.
考点：绝对值不等式.
练习册系列答案
相关题目
不等式组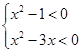
的解集是（ ）
| A．{x|0<x<1} | B．{x|－1<x<1} | C．{x|0<x<3} | D．{x|－1<x<3} |
若关于
的方程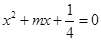
有两个不相等的实数根，则实数
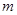的取值范围是（ ）
A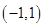． | B． |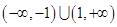
C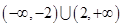． | D． |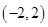
若不等式
的解集是
，那么
的值是 ( )
| A．1 | B．2 | C．3 | D．4 |
关于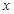
的不等式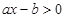
的解集是
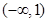，则关于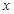的不等式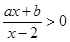
的解为（ ）
A． | B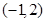． | C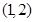． | D． |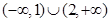
[2013·浙江高考]已知a，b，c∈R，函数f(x)＝ax2＋bx＋c.若f(0)＝f(4)>f(1)，则( )
| A．a>0,4a＋b＝0 | B．a<0,4a＋b＝0 |
| C．a>0,2a＋b＝0 | D．a<0,2a＋b＝0 |
若关于x的不等式|a|≥|x＋1|＋|x－2|存在实数解，则实数a的取值范围是( )
| A．[3，+∞) |
| B．(－∞，3] |
| C．(-1,2) |
| D．(-2,3] |
设函数f(x)=
，已知f(a)＞1，则a的取值范围是( )
A．(－∞，－2)∪( ，+∞) |
B．(， ) |
| C．(－∞，－2)∪(，1) |
| D．(－2，)∪(1，+∞) |