题目内容
求下列不等式的解集
(Ⅰ)
(Ⅱ)
(Ⅰ) ;(Ⅱ)
;(Ⅱ) .
.
解析试题分析:(Ⅰ)这是一个含绝对值的不等式,解此类不等式一般可用零点分类讨论,化为解不等式组的问题,另外也可以将其变形为 ,然后两边平方转化为一元二次不等式求解;(Ⅱ)同样用零点分类讨论,化为解不等式组的问题,也可以利用
,然后两边平方转化为一元二次不等式求解;(Ⅱ)同样用零点分类讨论,化为解不等式组的问题,也可以利用 型不等式解法求解;
型不等式解法求解;
试题解析:(Ⅰ)解法1:原不等式等价于 或
或 或
或
这三个不等式组的解集分别为 ,
, ,
, ,所以原不等式的解集为
,所以原不等式的解集为 ; 5分
; 5分
解法2:原不等式等价于 ,两边平方整理得,
,两边平方整理得, ,解得
,解得 ,
,
所以原不等式的解集为 ; 5分
; 5分
(Ⅱ)解法1:原不等式等价于 或
或
这两个不等式组的解集分别为 ,
, ,所以原不等式的解集为
,所以原不等式的解集为 ; 10分
; 10分
解法2: 原不等式等价于 ,所以
,所以 或
或 ,
,
解得 或
或
所以原不等式的解集为 . 10分
. 10分
考点:含绝对值的不等式.

练习册系列答案
相关题目
若不等式x2+2x+a≥-y2-2y对实数x,y都成立,则实数a范围是
| A. a≥0 | B. a≥1 | C. a≥2 | D.a≥3 |
已知不等式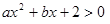 的解集为
的解集为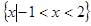 ,则不等式
,则不等式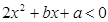 的解集为()
的解集为()
A.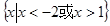 | B.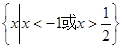 |
C.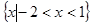 | D. |
对于实数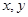 ,若
,若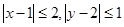 ,则
,则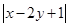 的最大值为( )
的最大值为( )
| A.4 | B.6 | C.8 | D.10 |
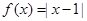 .
.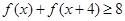 ;
;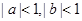 ,且
,且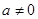 ,求证:
,求证: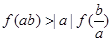 .
. .
.
 .
. 都是正数,且
都是正数,且
 ,若不等式
,若不等式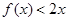 的解集为
的解集为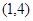 ,且方程
,且方程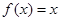 有两个相等的实数根.(1)求
有两个相等的实数根.(1)求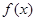 的解析式;(2)若不等式
的解析式;(2)若不等式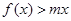 在
在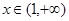 上恒成立,求实数
上恒成立,求实数 的取值范围;
的取值范围; 与
与 的大小.
的大小.