题目内容
在高等数学中有如下定义:函数y=f(x)的导数f′(x)叫作函数y=f(x)的一阶导数,类似地,把y=f′(x)的导数叫作函数y=f(x)的二阶导数.现若有函数f(x)=asinx+
bcosx+sin3x在x=
处取得极大值,则b的范围为( )
| 1 |
| 3 |
| π |
| 3 |
分析:根据二阶导数的定义,结合函数单调性与导数的关系,可得y=f(x)的极大值点x0满足:f'(x0)=0且二阶导数[f'(x0)]'<0.求出函数的导数和二阶导数,根据以上结论建立关于a、b的不等式,解之即得实数b的取值范围.
解答:解:函数y=f(x)在x=x0处取得极大值,说明y=f(x)在x=x0的左边为增函数,在x=x0的右边为减函数,
∴y=f'(x)在x=x0的左边为正数,在x=x0的右边为负数,得x=x0在y=f'(x)的减区间内
因此满足:f'(x0)=0且二阶导数[f'(x0)]'<0
对于函数f(x)=asinx+
bcosx+sin3x,得f'(x)=acosx-
bsinx+3cos3x
二阶导数[f'(x)]'=-asinx-
bcosx-9sin3x
∵函数f(x)=asinx+
bcosx+sin3x在x=
处取得极大值,
∴
,解之得:b<
故选A
∴y=f'(x)在x=x0的左边为正数,在x=x0的右边为负数,得x=x0在y=f'(x)的减区间内
因此满足:f'(x0)=0且二阶导数[f'(x0)]'<0
对于函数f(x)=asinx+
| 1 |
| 3 |
| 1 |
| 3 |
二阶导数[f'(x)]'=-asinx-
| 1 |
| 3 |
∵函数f(x)=asinx+
| 1 |
| 3 |
| π |
| 3 |
∴
|
| 3 |
故选A
点评:本题给出函数二阶导数的定义,求函数取得极大值时参数的取值范围,着重考查了函数单调性导数的关系与利用导数研究函数的极值等知识,属于基础题.

练习册系列答案
相关题目
 在平面向量中有如下定理:设点O、P、Q、R为同一平面内的点,则P、Q、R三点共线的充要条件是:存在实数t,使
在平面向量中有如下定理:设点O、P、Q、R为同一平面内的点,则P、Q、R三点共线的充要条件是:存在实数t,使 (2011•惠州二模)在平面向量中有如下定理:设点O,P,Q,R为同一平面内的点,则P,Q,R三点共线的充要条件是:存在实数t,使
(2011•惠州二模)在平面向量中有如下定理:设点O,P,Q,R为同一平面内的点,则P,Q,R三点共线的充要条件是:存在实数t,使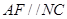 ;②
;②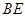 与
与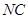 是异面直线;③
是异面直线;③ 与
与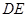 成
成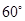 角;④
角;④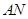 与
与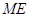 成
成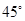 角。其中正确命题为 .(填正确命题的序号)
角。其中正确命题为 .(填正确命题的序号)