题目内容
已知函数 ,曲线
,曲线 在点
在点 处的切线为
处的切线为 ,若
,若 时,
时, 有极值.
有极值.
(1)求 的值;
的值;
(2)求 在
在 上的最大值和最小值.
上的最大值和最小值.
 ,曲线
,曲线 在点
在点 处的切线为
处的切线为 ,若
,若 时,
时, 有极值.
有极值.(1)求
 的值;
的值;(2)求
 在
在 上的最大值和最小值.
上的最大值和最小值.(1)由 得,
得,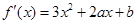 1分
1分
当 时,切线
时,切线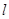 的斜率为3,可得
的斜率为3,可得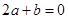 ① 2分
① 2分
当 时,
时, 有极值,得
有极值,得 3分
3分
可得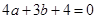 ②
②
由①②解得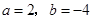 4分
4分
由于切点的横坐标为 ∴
∴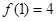
∴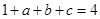
∴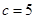 5分
5分
(2)由(1)可得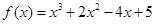
∴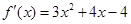 6分
6分
令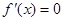 ,得
,得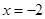 ,
, 7分
7分
当 变化时,
变化时,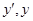 的取值及变化如下表:
的取值及变化如下表:
真确列出表得 9分
∴ y=f(x)在[-3,1]上的最大值为13,最小值为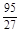
 得,
得,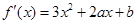 1分
1分当
 时,切线
时,切线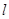 的斜率为3,可得
的斜率为3,可得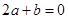 ① 2分
① 2分当
 时,
时, 有极值,得
有极值,得 3分
3分可得
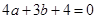 ②
②由①②解得
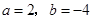 4分
4分由于切点的横坐标为
 ∴
∴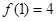
∴
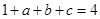
∴
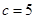 5分
5分(2)由(1)可得
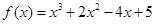
∴
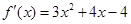 6分
6分令
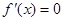 ,得
,得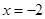 ,
, 7分
7分当
 变化时,
变化时,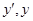 的取值及变化如下表:
的取值及变化如下表: 真确列出表得 9分
 | 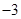 | 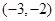 | 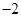 | 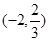 | 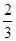 | 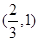 | 1 |
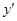 | | + | 0 | - | 0 | + | |
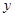 | 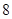 |   | 13 |  | 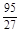 |  | 4 |
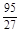
(1)根据 可建立关于a,b,c的三个方程,解方程组即可.
可建立关于a,b,c的三个方程,解方程组即可.
(2)在(1)的基础上,利用导数列表求极值,最值即可.
 可建立关于a,b,c的三个方程,解方程组即可.
可建立关于a,b,c的三个方程,解方程组即可.(2)在(1)的基础上,利用导数列表求极值,最值即可.

练习册系列答案
相关题目
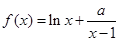 在
在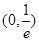 内有极值.
内有极值.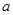 的取值范围;
的取值范围;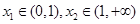 求证:
求证: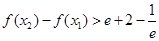 .
.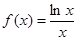 ,若方程
,若方程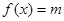 存在两个不同的实数解,则实数
存在两个不同的实数解,则实数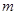 的取值范围为( ▲ )
的取值范围为( ▲ )



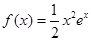 .
.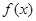 的单调区间;
的单调区间; 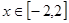 时,不等式
时,不等式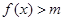 恒成立,求实数
恒成立,求实数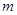 的取值范围.
的取值范围.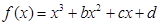 图象如图,则函数
图象如图,则函数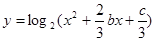
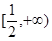
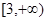
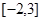
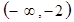
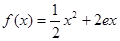 ,
,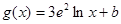 (其中
(其中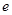 为常数,
为常数,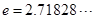 ),若这两个函数的图象有公共点,且在该点处的切线相同。
),若这两个函数的图象有公共点,且在该点处的切线相同。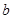 的值;
的值;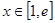 时,
时, 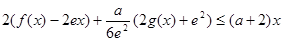 恒成立,求实数
恒成立,求实数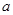 的取值范围.
的取值范围. 在其定义域内的一个子区间
在其定义域内的一个子区间 内是单调函数,则实数
内是单调函数,则实数 的取值范围是________ ____
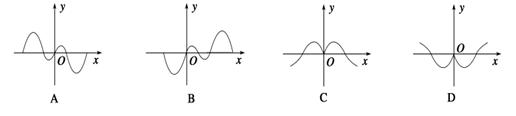
的取值范围是________ ____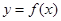 的图象如右图所示,那么导函数
的图象如右图所示,那么导函数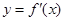 的图象可能是( )
的图象可能是( )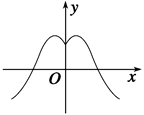
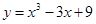 的极小值是 .
的极小值是 .