题目内容
已知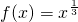 x∈[-1,8],
x∈[-1,8], .若对任意x1∈[-1,8],总存在
.若对任意x1∈[-1,8],总存在 ,使得f(x1)≥g(x2)成立,则实数a的取值范围是________.
,使得f(x1)≥g(x2)成立,则实数a的取值范围是________.
a≥4或a≤-2
分析:若对任意x1∈[-1,8],总存在 ,使得f(x1)≥g(x2)成立,可以转化为f(x)min≥g(x)max,从而问题得解.
,使得f(x1)≥g(x2)成立,可以转化为f(x)min≥g(x)max,从而问题得解.
解答:若对任意x1∈[-1,8],总存在 ,使得f(x1)≥g(x2)成立,可以转化为f(x)min≥g(x)max,
,使得f(x1)≥g(x2)成立,可以转化为f(x)min≥g(x)max,
由于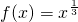 是x∈[-1,8]上的单调增函数,∴f(x)min=-1
是x∈[-1,8]上的单调增函数,∴f(x)min=-1
 ,∵
,∵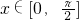 ,∴
,∴ ,∴
,∴ ,∴
,∴ ,当a>0时,
,当a>0时, ,当a<0时,
,当a<0时, ,故可求实数a的取值范围是a≥4或a≤-2,故答案为a≥4或a≤-2.
,故可求实数a的取值范围是a≥4或a≤-2,故答案为a≥4或a≤-2.
点评:本题主要考查函数恒成立问题,考查利用函数的最值,有一定的技巧.
分析:若对任意x1∈[-1,8],总存在
 ,使得f(x1)≥g(x2)成立,可以转化为f(x)min≥g(x)max,从而问题得解.
,使得f(x1)≥g(x2)成立,可以转化为f(x)min≥g(x)max,从而问题得解.解答:若对任意x1∈[-1,8],总存在
 ,使得f(x1)≥g(x2)成立,可以转化为f(x)min≥g(x)max,
,使得f(x1)≥g(x2)成立,可以转化为f(x)min≥g(x)max,由于
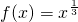 是x∈[-1,8]上的单调增函数,∴f(x)min=-1
是x∈[-1,8]上的单调增函数,∴f(x)min=-1 ,∵
,∵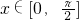 ,∴
,∴ ,∴
,∴ ,∴
,∴ ,当a>0时,
,当a>0时, ,当a<0时,
,当a<0时, ,故可求实数a的取值范围是a≥4或a≤-2,故答案为a≥4或a≤-2.
,故可求实数a的取值范围是a≥4或a≤-2,故答案为a≥4或a≤-2.点评:本题主要考查函数恒成立问题,考查利用函数的最值,有一定的技巧.

练习册系列答案
相关题目
 x∈[-1,8],
x∈[-1,8], .若对任意x1∈[-1,8],总存在
.若对任意x1∈[-1,8],总存在 ,使得f(x1)≥g(x2)成立,则实数a的取值范围是 .
,使得f(x1)≥g(x2)成立,则实数a的取值范围是 . x∈[-1,8],
x∈[-1,8], .若对任意x1∈[-1,8],总存在
.若对任意x1∈[-1,8],总存在 ,使得f(x1)≥g(x2)成立,则实数a的取值范围是 .
,使得f(x1)≥g(x2)成立,则实数a的取值范围是 .