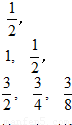题目内容
 .如图所示给出一个“三角形数阵”,已知每一列的数成等差数列,从第三行起,每一行的数成等比数列,每一行的公比都相等,记第i行第j列的数为aij(i≥j,j∈N+),则a83=( )
.如图所示给出一个“三角形数阵”,已知每一列的数成等差数列,从第三行起,每一行的数成等比数列,每一行的公比都相等,记第i行第j列的数为aij(i≥j,j∈N+),则a83=( )分析:先确定ai1,再求出aij=i×(
)j,即可得到结论.
| 1 |
| 2 |
解答:解:由题意,每一列的数成等差数列,首项
,公差为
∴ai1=
+(i-1)•
=
,
每一行的数成等比数列,公比为
,∴aij=ai1×(
)j-1=
×(
)j-1=i×(
)j.
∴a83=8×(
)3=1
故选D.
| 1 |
| 2 |
| 1 |
| 2 |
∴ai1=
| 1 |
| 2 |
| 1 |
| 2 |
| i |
| 2 |
每一行的数成等比数列,公比为
| 1 |
| 2 |
| 1 |
| 2 |
| i |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴a83=8×(
| 1 |
| 2 |
故选D.
点评:本题考查等差数列和等比数列的性质,考查了考生分析问题和解决问题的能力,属于中档题.

练习册系列答案
相关题目
 如图所示给出的是计算
如图所示给出的是计算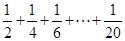 的值的一个程序框图,其中判断框内可以填的条件是( )
的值的一个程序框图,其中判断框内可以填的条件是( )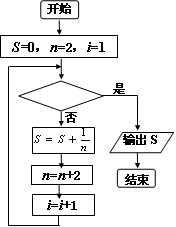
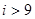 B.
B.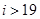 C.
C.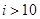 D.
D.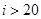
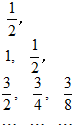 .如图所示给出一个“三角形数阵”,已知每一列的数成等差数列,从第三行起,每一行的数成等比数列,每一行的公比都相等,记第i行第j列的数为aij(i≥j,j∈N+),则a83=
.如图所示给出一个“三角形数阵”,已知每一列的数成等差数列,从第三行起,每一行的数成等比数列,每一行的公比都相等,记第i行第j列的数为aij(i≥j,j∈N+),则a83=