题目内容
若A、B是锐角△ABC的两个内角,则点P(cosB-sinA,sinB-cosA)在第________象限.
二
分析:由题意知A、B、C是锐角,推出A、B的关系,分别求它的正弦和余弦,即可得到结果.
解答:在锐角三角形ABC中,有A<90°,B<90°,C<90°,
又因为A+B+C=180°所以有A+B>90°,
所以有A>90°-B.
又因为Y=cosx在0°<x<90°上单调减即cosx的值随x的增加而减少,
所以有cosA<cos(90°-B)=sinB,
即cosA<sinB,sinB-cosA>0
同理B>90°-A,则cosB<cos(90°-A)=sinA,所以cosB-sinA<0
故答案为:二.
点评:本题考查三角形内角,象限角等知识,是中档题.
分析:由题意知A、B、C是锐角,推出A、B的关系,分别求它的正弦和余弦,即可得到结果.
解答:在锐角三角形ABC中,有A<90°,B<90°,C<90°,
又因为A+B+C=180°所以有A+B>90°,
所以有A>90°-B.
又因为Y=cosx在0°<x<90°上单调减即cosx的值随x的增加而减少,
所以有cosA<cos(90°-B)=sinB,
即cosA<sinB,sinB-cosA>0
同理B>90°-A,则cosB<cos(90°-A)=sinA,所以cosB-sinA<0
故答案为:二.
点评:本题考查三角形内角,象限角等知识,是中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
若A,B是平面内的两个定点,点P为该平面内动点,且满足向量
与
夹角为锐角θ,|
||
|+
•
=0,则点P的轨迹是( )
| AB |
| AP |
| PB |
| AB |
| PA |
| AB |
| A、直线(除去与直线AB的交点) |
| B、圆(除去与直线AB的交点) |
| C、椭圆(除去与直线AB的交点) |
| D、抛物线(除去与直线AB的交点) |
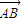 与
与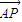 夹角为锐角θ,
夹角为锐角θ,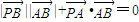 ,则点P的轨迹是( )
,则点P的轨迹是( )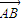 与
与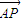 夹角为锐角θ,
夹角为锐角θ, ,则点P的轨迹是( )
,则点P的轨迹是( )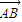 与
与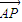 夹角为锐角θ,
夹角为锐角θ,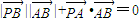 ,则点P的轨迹是( )
,则点P的轨迹是( )