题目内容
若A,B是平面内的两个定点,点P为该平面内动点,且满足向量
与
夹角为锐角θ,|
||
|+
•
=0,则点P的轨迹是( )
| AB |
| AP |
| PB |
| AB |
| PA |
| AB |
| A、直线(除去与直线AB的交点) |
| B、圆(除去与直线AB的交点) |
| C、椭圆(除去与直线AB的交点) |
| D、抛物线(除去与直线AB的交点) |
分析:以AB所在直线为x轴,AB的垂直平分线为y轴,建立平面直角坐标系,先设P(x,y),欲动点P的轨迹C的方程,即寻找x,y之间的关系,结合向量的坐标运算即可得到.
解答:解:以AB所在直线为x轴,AB的垂直平分线为y轴,建立平面直角坐标系,
设A(-a,0),B(a,0),P(x,y),
则
=(2a,0),
=(x+a,y),
=(a-x,-y),代入
|
||
|+
•
=0得2a
-2a(x+a)=0;
整理得y2=4ax,
故点P的轨迹是抛物线(除去与直线AB的交点),
故选D.
设A(-a,0),B(a,0),P(x,y),
则
| AB |
| AP |
| PB |
|
| PB |
| AB |
| PA |
| AB |
| (a-x)2+y2 |
整理得y2=4ax,
故点P的轨迹是抛物线(除去与直线AB的交点),
故选D.
点评:此题是个基础题.求曲线的轨迹方程是解析几何的基本问题 求符合某种条件的动点的轨迹方程,其实质就是利用题设中的几何条件,用“坐标化”将其转化为寻求变量间的关系.

练习册系列答案
相关题目
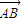 与
与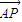 夹角为锐角θ,
夹角为锐角θ,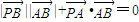 ,则点P的轨迹是( )
,则点P的轨迹是( )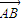 与
与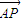 夹角为锐角θ,
夹角为锐角θ, ,则点P的轨迹是( )
,则点P的轨迹是( )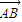 与
与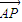 夹角为锐角θ,
夹角为锐角θ,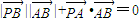 ,则点P的轨迹是( )
,则点P的轨迹是( )