题目内容
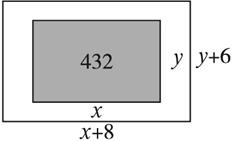
一份印刷品,其排版面积(矩形)为432 cm2,它的左,右两边都留有4 cm的空白,上,下都留有3 cm的空白,问长,宽各设计成多少厘米时,用纸最省?并求出此时纸面的面积.
解:如图,设排版面积的矩形长为x cm,宽为ycm,则印刷品用纸的长为(x+8) cm,宽为(y+6) cm,记其面积为S,则
![]()
∴S=xy+6x+8y+48=432+48+6x+8y≥480+2![]() =480+2
=480+2![]() =768(cm2).?
=768(cm2).?
当且仅当6x=8y时等号成立,?
即6x2=8xy=8×432,?
∴x2=576.∴x=24,y=18.?
∴纸面长为x+8=32 cm,纸面宽为y+6=24cm,这张纸面的面积为768 cm2

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,一份印刷品的排版面积(矩形)为A,它的两边都留有宽为a的空白,顶部和底部都留有宽为b的空白.则当纸张的长和宽分别为多少时,才能使纸的用量最少?
如图,一份印刷品的排版面积(矩形)为A,它的两边都留有宽为a的空白,顶部和底部都留有宽为b的空白.则当纸张的长和宽分别为多少时,才能使纸的用量最少?
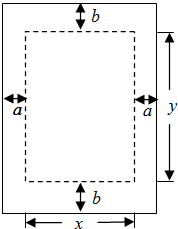 如图,一份印刷品的排版面积(矩形)为A,它的两边都留有宽为a的空白,顶部和底部都留有宽为b的空白.则当纸张的长和宽分别为多少时,才能使纸的用量最少?
如图,一份印刷品的排版面积(矩形)为A,它的两边都留有宽为a的空白,顶部和底部都留有宽为b的空白.则当纸张的长和宽分别为多少时,才能使纸的用量最少?