题目内容
 如图,一份印刷品的排版面积(矩形)为A,它的两边都留有宽为a的空白,顶部和底部都留有宽为b的空白.则当纸张的长和宽分别为多少时,才能使纸的用量最少?
如图,一份印刷品的排版面积(矩形)为A,它的两边都留有宽为a的空白,顶部和底部都留有宽为b的空白.则当纸张的长和宽分别为多少时,才能使纸的用量最少?分析:设出排版矩形的长和宽,表示出纸张的面积,利用基本不等式求最值,即可得到结论.
解答:解:设排版矩形的长和宽分别是x,y,则xy=A
纸张的面积为:S=(x+2a)(x+2b)=xy+2bx+2ay+4ab≥xy+2
+4ab=(
+2
)2
当且仅当2bx=2ay,即x=
,y=
时,S有最小值(
+2
)2,此时纸张的长和宽分别为
+2a,
+2b.
答:当纸张的长和宽分别为
+2a和
+2b时,纸张的用量最少
纸张的面积为:S=(x+2a)(x+2b)=xy+2bx+2ay+4ab≥xy+2
| 4abxy |
| A |
| ab |
当且仅当2bx=2ay,即x=
|
|
| A |
| ab |
|
|
答:当纸张的长和宽分别为
|
|
点评:本题考查函数模型的构建,考查利用基本不等式求最值,表示出纸张的面积是关键.

练习册系列答案
 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案
相关题目
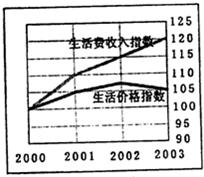 8、如图是一份从2000年初到2003年初的统计图表,根据此图表得到以下说法中,正确的有( )
8、如图是一份从2000年初到2003年初的统计图表,根据此图表得到以下说法中,正确的有( ) 9、如图是一份统计图表,根据此图表得到的以下说法中,正确的是
9、如图是一份统计图表,根据此图表得到的以下说法中,正确的是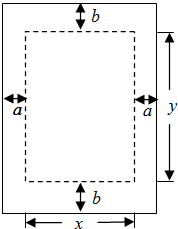 如图,一份印刷品的排版面积(矩形)为A,它的两边都留有宽为a的空白,顶部和底部都留有宽为b的空白.则当纸张的长和宽分别为多少时,才能使纸的用量最少?
如图,一份印刷品的排版面积(矩形)为A,它的两边都留有宽为a的空白,顶部和底部都留有宽为b的空白.则当纸张的长和宽分别为多少时,才能使纸的用量最少?