题目内容
已知各项均为正数的等比数列{an}的前n项和为Sn,a1=3,S3=39.(1)求数列{an}通项公式;
(2)若在an与an+1之间插入n个数,使得这n+2个数组成一个公差为dn的等差数列,求证:
 …
… .
.
【答案】分析:(Ⅰ)由a1=3,S3=39,知1+q+q2=13.故q=3,或q=-4,由此能求出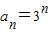 .
.
(Ⅱ)由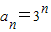 ,知
,知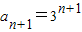 ,由题知:an+1=an+(n+1)dn,则
,由题知:an+1=an+(n+1)dn,则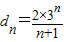 .由上知:
.由上知: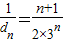 ,所以
,所以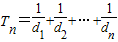 =
=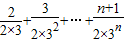 ,由此利用错位相减法能够证明
,由此利用错位相减法能够证明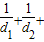 …
…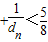 .
.
解答:解:(Ⅰ)∵a1=3,S3=39,∴q≠1,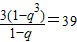 ,
,
∴1+q+q2=13.∴q=3,或q=-4(舍),
故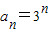 .…(6分)
.…(6分)
(Ⅱ)∵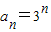 ,则
,则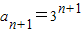 ,由题知:
,由题知:
an+1=an+(n+1)dn,则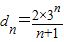 .
.
由上知: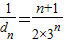 ,
,
所以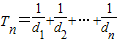 =
=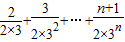 ,
,
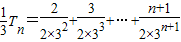 ,
,
所以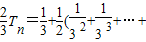
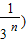 -
-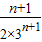
=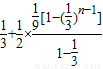 -
-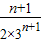
=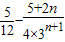 ,
,
所以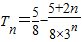
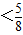 .
.
故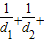 …
…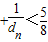 .…(12分)
.…(12分)
点评:本题考查数列通项公式的求法,证明数列的前n项和小于定值.综合性强,难度大,有一定的探索性,对数学思维能力要求较高,是高考的重点.解题时要认真审题,仔细解答,注意错位相减法的合理运用.
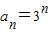 .
.(Ⅱ)由
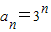 ,知
,知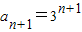 ,由题知:an+1=an+(n+1)dn,则
,由题知:an+1=an+(n+1)dn,则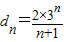 .由上知:
.由上知: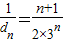 ,所以
,所以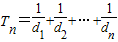 =
=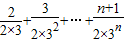 ,由此利用错位相减法能够证明
,由此利用错位相减法能够证明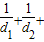 …
…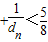 .
.解答:解:(Ⅰ)∵a1=3,S3=39,∴q≠1,
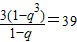 ,
,∴1+q+q2=13.∴q=3,或q=-4(舍),
故
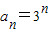 .…(6分)
.…(6分)(Ⅱ)∵
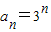 ,则
,则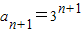 ,由题知:
,由题知:an+1=an+(n+1)dn,则
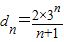 .
.由上知:
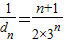 ,
,所以
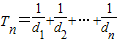 =
=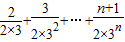 ,
,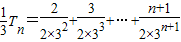 ,
,所以
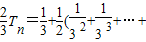
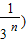 -
-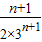
=
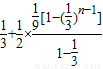 -
-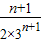
=
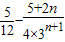 ,
,所以
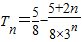
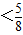 .
.故
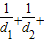 …
…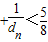 .…(12分)
.…(12分)点评:本题考查数列通项公式的求法,证明数列的前n项和小于定值.综合性强,难度大,有一定的探索性,对数学思维能力要求较高,是高考的重点.解题时要认真审题,仔细解答,注意错位相减法的合理运用.

练习册系列答案
相关题目
 ,
, 的等比中项。
的等比中项。 是等差数列;(2)若
是等差数列;(2)若 的前n项和为Tn,求Tn。
的前n项和为Tn,求Tn。 中,
中, 与
与 的等比中项为
的等比中项为 ,则
,则 的最小值为( )
的最小值为( ) ,
, 的等比中项。
的等比中项。 是等差数列;(2)若
是等差数列;(2)若 的前n项和为Tn,求Tn。
的前n项和为Tn,求Tn。 ,
, 的等比中项。
的等比中项。 是等差数列;
是等差数列; 的前n项和为Tn,求Tn。
的前n项和为Tn,求Tn。 ,
, 的等比中项。
的等比中项。 是等差数列;(2)若
是等差数列;(2)若 的前n项和为Tn,求Tn。
的前n项和为Tn,求Tn。