题目内容
(12分)已知函数f(x)＝cos(2x－)＋2sin(x－)sin(x＋)．
(1)求函数f(x)的最小正周期； (2)求函数f(x)在区间[－，]上的值域．
【答案】
解：(1)f(x)＝cos(2x－)＋2sin(x－)sin(x＋)
＝cos2x＋sin2x＋2·(sinx－cosx)·(sinx＋cosx)
＝cos2x＋sin2x－cos2x
＝sin2x－cos2x
＝sin2xcos－cos2xsin
＝sin(2x－)．
∴T＝＝π.
(2)∵x∈[－，]，∴2x－∈[－，π]．
∵f(x)＝sin(2x－)在区间[－，]上单调递增，在区间[，]上单调递减，
∴当x＝时，f(x)取得最大值1.又∵f(－)＝－＜＝f()，
∴当x＝－时，f(x)取得最小值－.
∴f(x)的值域为[－，1]．
【解析】略
练习册系列答案
名校课堂系列答案
相关题目
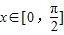，求f（x）的最大值，最小值．
（x∈R），Ｐ1（ｘ1，ｙ1），Ｐ2（ｘ2，ｙ2）是函数ｙ＝ｆ(x)图像上两点，且线段Ｐ1Ｐ2中点Ｐ的横坐标为
。
｝的通项公式为
)(ｍ∈Ｎ
，ｎ＝１,２,３,…,ｍ），求数列｛
； （5分）
＜
横成立，求实数a的取值范围。（3分）
)=
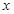,当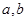
的值及函数f(
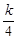f(
，问