题目内容
已知椭圆
＝1(a>b>0)的离心率e＝
，连结椭圆的四个顶点得到的菱形的面积为4.
(1)求椭圆的方程；
(2)设直线l与椭圆相交于不同的两点A，B.已知点A的坐标为(－a，0)．若|AB|＝
，求直线l的倾斜角．
＝1(a>b>0)的离心率e＝，连结椭圆的四个顶点得到的菱形的面积为4.(1)求椭圆的方程；
(2)设直线l与椭圆相交于不同的两点A，B.已知点A的坐标为(－a，0)．若|AB|＝
，求直线l的倾斜角．（1）
＋y2＝1（2）
或
＋y2＝1（2）或(1)由e＝
＝，解得3a2＝4c2.再由c2＝a2－b2，解得a＝2b.
由题意可知
×2a×2b＝4，即ab＝2.解方程组
得
所以椭圆的方程为＋y2＝1.
(2)由(1)可知点A(－2，0)，设点B的坐标为(x1，y1)，直线l的斜率为k，则直线l的方程为y＝k(x＋2)．于是A、B两点的坐标满足方程组
消去y并整理，得(1＋4k2)x2＋16k2x＋(16k2－4)＝0，
由－2x1＝
，得x1＝
，从而y1＝
，
故|AB|＝
＝
.
由|AB|＝，得＝.整理得32k4－9k2－23＝0，
即(k2－1)(32k2＋23)＝0，解得k＝±1.所以直线l的倾斜角为或
＝，解得3a2＝4c2.再由c2＝a2－b2，解得a＝2b.由题意可知
×2a×2b＝4，即ab＝2.解方程组得所以椭圆的方程为
＋y2＝1.(2)由(1)可知点A(－2，0)，设点B的坐标为(x1，y1)，直线l的斜率为k，则直线l的方程为y＝k(x＋2)．于是A、B两点的坐标满足方程组
消去y并整理，得(1＋4k2)x2＋16k2x＋(16k2－4)＝0，
由－2x1＝
，得x1＝，从而y1＝，故|AB|＝
＝.由|AB|＝
，得＝.整理得32k4－9k2－23＝0，即(k2－1)(32k2＋23)＝0，解得k＝±1.所以直线l的倾斜角为
或
练习册系列答案
阳光课堂同步练习系列答案
相关题目
的椭圆
上求一点Q，使该点到直线（
的距离最大。
的左、右焦点分别为
、
， 焦距为2，过
为3 
交椭圆于A、B两点，判断是否存在直线
为钝角，若存在，求出直线
的取值范围
＝1(a＞b＞0)的离心率为
，且过点A(0，1)．
.
＋y2＝1的两焦点为F1，F2，点P(x0，y0)满足
＋
≤1，则PF1＋PF2的取值范围为________．
分别是椭圆的左，右焦点，现以
为圆心作一个圆恰好经过椭圆中心并且交椭圆于点
，若过
的直线
是圆
＋y2＝1的左右焦点，点P在椭圆上运动．则
的最大值是________．
，焦距为2
；
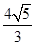和
，过P点作长轴的垂线恰好过椭圆的一个焦点．
+
=1(a>b>0)与抛物线y2=2px(p>0)有相同的焦点,P、Q是椭圆与抛物线的交点,若PQ经过焦点F,则椭圆