题目内容
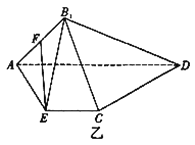
【题目】如图,已知四棱锥![]() 的底面为菱形,且
的底面为菱形,且![]() ,
,![]() 是
是![]() 中点.
中点.
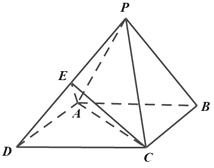
(1)证明:![]() 平面
平面![]() ;
;
(2)若![]() ,
,![]() ,求三棱锥
,求三棱锥![]() 的体积.
的体积.
【答案】(1)证明见解析 (2)![]()
【解析】
(1)连接BD交AC于F,连接EF,证明EF∥PB得到结论.
(2)先确定AP⊥BP且△ABC为正三角形,取AB中点M,连接PM、CM,证明PM⊥平面ABCD,根据![]() 得到答案.
得到答案.
(1)连接BD交AC于F,连接EF
∵四边形ABCD为菱形,∴F为AC中点,那么EF∥PB
又∵![]() 平面ACE,
平面ACE,![]() 平面ACE∴PB∥平面ACE;
平面ACE∴PB∥平面ACE;

(2)由勾股定理易知AP⊥BP且△ABC为正三角形,
∵E为DP中点,∴![]() ,
,
取AB中点M,连接PM、CM,由几何性质可知PM=1,![]() ,
,
又∵PC=2,∴PC2=PM2+MC2,即PM⊥MC,∵PM⊥AB,
∴PM⊥平面ABCD,
∴![]() ,∴
,∴![]() .
.

练习册系列答案
相关题目