题目内容
如图，在四面体
中，
，
，
，且
。
⑴设
是
的中点，
在
上且
，证明：
；
⑵求二面角
的平面角的余弦值。
⑴证明：过
点在平面
内作
，分别以
、
、
为
轴、
轴、
轴建立空间直角坐标系。则
，
，
，
，
，
则设
，由
则
，
，
即
。
⑵依题意有：面
的法向量为
。
,
设面
的法向量为
由
即
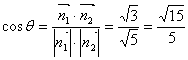
由于二面角的平面角是锐角，所以二面角的平面角的余弦值为
。
练习册系列答案
相关题目
题目内容
如图，在四面体中，，，，且。
⑴设是的中点，在上且，证明：；
⑵求二面角的平面角的余弦值。
⑴证明：过点在平面内作，分别以、、为轴、轴、轴建立空间直角坐标系。则，，，，，
则设，由则，
，即。
⑵依题意有：面的法向量为。
,
设面的法向量为
由
即
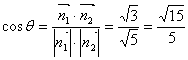
由于二面角的平面角是锐角，所以二面角的平面角的余弦值为。
中，截面
是正方形，则下列命题:
.②
∥截面
与
所成的角为
.
中，截面
是正方形，则在下列命题中，错误的为（ ）
∥截面
与
所成的角为
中,
，
，且
为线段
的中点，试在线段
上求一点
，使得
；
的平面角的余弦值.
中，截面
是正方形，则在下列命题中，错误的为（
）
∥截面
与
所成的角为
中，
平面
，
，
，
，
是
的中点；
；
与平面