题目内容
(本小题满分12分)如图,在四面体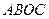 中,
中,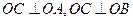 ,
,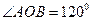 ,且
,且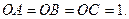
(I)设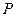 为线段
为线段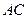 的中点,试在线段
的中点,试在线段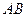 上求一点
上求一点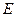 ,使得
,使得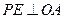
 ;
;
(II)求二面角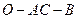 的平面角的余弦值.
的平面角的余弦值.
解:在平面内 过点
过点 作
作 交
交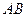 于点
于点 .
.
以 为坐标原点,分别以
为坐标原点,分别以 、
、 、
、 所在直线为
所在直线为 轴、
轴、 轴、
轴、 轴,建立空间直角坐标系(如图). ………………………………………………………………………1分
轴,建立空间直角坐标系(如图). ………………………………………………………………………1分
则 、
、 、
、 、
、 . ……………………….…..3分
. ……………………….…..3分
(I)设 ,因为
,因为 ,
,
所以 ,
, .
.
因为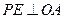 ,所以
,所以 . 即
. 即 ,解得
,解得 .
.
故所求点为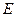
 .
.
即点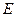 为线段
为线段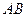 的三等分点(靠近点
的三等分点(靠近点 ). ………………………………………7分
). ………………………………………7分
(II)设平面 的法向量为
的法向量为 ,
, .
.
由 得
得 .
.
令 得
得 . 即
. 即 . …………………………………………..9分
. …………………………………………..9分
又 是平面
是平面 的法向量, ………………………………………………10分
的法向量, ………………………………………………10分
所以 .
.
故二面角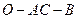 的平面角的余弦值为
的平面角的余弦值为 . ……………………………………12分
. ……………………………………12分
解析

练习册系列答案
 华东师大版一课一练系列答案
华东师大版一课一练系列答案
相关题目