题目内容
已知函数
 为偶函数,且
为偶函数,且 .
.
(1)
求m的值,并确定 的解析式;
的解析式;
(2)
若 ,是否存在实数a,使
,是否存在实数a,使 在区间[2,3]上为增函数.
在区间[2,3]上为增函数.
答案:略
解析:
提示:
解析:
|
(1) 由 得 得
∵  在 在 上为减函数, 上为减函数,
∴  . .
∵  ,∴m=0或m=1. ,∴m=0或m=1.
当 m=0时, ; ;
当 m=1时, . .
而  为偶函数,∴m=1,此时 为偶函数,∴m=1,此时 . .
(2) 假设存在实数a,使 在区间[2,3]上为增函数. 在区间[2,3]上为增函数.
则由  与 与 存在,得 存在,得 , , . .
令  ,则 ,则 开口向上,对称轴 开口向上,对称轴 . .
∴当  时 时 为增函数,又由 为增函数,又由 在区间[2,3]上为增函数,得a>1,∴1<a<2. 在区间[2,3]上为增函数,得a>1,∴1<a<2. |
提示:
|
问题的解决往往依赖于对条件或结论的转化.对于 (1),应首先转化较为复杂的条件.如果从偶函数的角度开始转化,不论是用偶函数的定义还是用幂函数中的偶函数,都难以找到进一步转化的途径.但从 入手,就不难把转化连续进行下去.对于(2),由于(1)中没有附加的条件,因而可以利用(1)的结论转化(2)的附加条件,并利用单调函数的性质使问题得到解决. 入手,就不难把转化连续进行下去.对于(2),由于(1)中没有附加的条件,因而可以利用(1)的结论转化(2)的附加条件,并利用单调函数的性质使问题得到解决. |

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

 的值.
的值. 的值。
的值。 为偶函数,且
为偶函数,且 在
在 上递减,设
上递减,设 ,
, ,
, ,则
,则 的大小关系正确的是( )
的大小关系正确的是( ) (B)
(B) (C)
(C) (D)
(D)
 为偶函数,且在
为偶函数,且在 上为增函数.
上为增函数. 的值,并确定
的值,并确定 的解析式;
的解析式; 且
且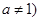 ,是否存在实数
,是否存在实数 使
使 在区间
在区间 上的最大值为2,若存在,求出
上的最大值为2,若存在,求出 的值,若不存在,请说明理由.
的值,若不存在,请说明理由. 为偶函数, 且
为偶函数, 且
 的值;
的值; 为三角形
为三角形 的一个内角,求满足
的一个内角,求满足 的
的