题目内容
(本小题满分10分)已知函数 为偶函数,且在
为偶函数,且在 上为增函数.
上为增函数.
(1)求 的值,并确定
的值,并确定 的解析式;
的解析式;
(2)若 且
且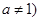 ,是否存在实数
,是否存在实数 使
使 在区间
在区间 上的最大值为2,若存在,求出
上的最大值为2,若存在,求出 的值,若不存在,请说明理由.
的值,若不存在,请说明理由.
【答案】
(1) 或
或 ,
,
(2) 存在实数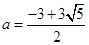 ,使
,使 在区间
在区间 上的最大值为2
上的最大值为2
【解析】
试题分析:(1)由条件幂函数 ,在
,在 上为增函数,
上为增函数,
得到 
解得 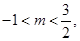 2分
2分
又因为 
所以 或
或 3分
3分
又因为是偶函数
当 时,
时, 不满足
不满足 为奇函数;
为奇函数;
当 时,
时, 满足
满足 为偶函数;
为偶函数;
所以 5分
5分
(2) 令
令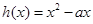 ,
,
由 得:
得:
 在
在 上有定义,
上有定义, 且
且
 在
在 上为增函数.
7分
上为增函数.
7分
当 时,
时,

因为 所以
所以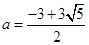 8分
8分
当 时,
时,

 此种情况不存在, 9分
此种情况不存在, 9分
综上,存在实数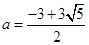 ,使
,使 在区间
在区间 上的最大值为2 10分
上的最大值为2 10分
考点:函数的基本性质运用。
点评:解决该试题的关键是能理解函数的奇偶性和单调性的运用,能理解复合函数的性质得到最值,属于基础题。

练习册系列答案
 快捷英语周周练系列答案
快捷英语周周练系列答案
相关题目
 (选做题)本题包括A、B、C、D四小题,请选定其中两题,并在答题卡指定区域内作答,若多做,则按作答的前两题评分,解答时应写出文字说明、证明过程或演算步骤.
(选做题)本题包括A、B、C、D四小题,请选定其中两题,并在答题卡指定区域内作答,若多做,则按作答的前两题评分,解答时应写出文字说明、证明过程或演算步骤. 本题包括(1)、(2)、(3)、(4)四小题,请选定其中两题,并在答题卡指定区域内答,
本题包括(1)、(2)、(3)、(4)四小题,请选定其中两题,并在答题卡指定区域内答,