题目内容
7.定义在R上的函数f(x)对任意x1、x2(x1≠x2)都有$\frac{f({x}_{1})-f({x}_{2})}{{x}_{1}-{x}_{2}}$<0,且函数y=f(x-1)的图象关于(1,0)成中心对称,若s,t满足不等式f(s2-2s)≤-f(2t-t2),则当1≤s≤4时,$\frac{t-2s}{s+t}$的取值范围是( )| A. | [-3,-$\frac{1}{2}$) | B. | [-3,-$\frac{1}{2}$] | C. | [-5,-$\frac{1}{2}$) | D. | [-5,-$\frac{1}{2}$] |
分析 根据已知条件便可得到f(x)在R上是减函数,且是奇函数,所以由不等式f(s2-2s)≤-f(2t-t2)便得到,s2-2s≥t2-2t,将其整理成(s-t)(s+t-2)≥0,画出不等式组$\left\{\begin{array}{l}{(s-t)(s+t-2)≥0}\\{1≤s≤4}\end{array}\right.$所表示的平面区域.设$\frac{t-2s}{s+t}=z$,所以得到t=$\frac{z+2}{1-z}s$,通过图形求关于s的一次函数的斜率范围即可得到z的范围,从而求出$\frac{t-2s}{s+t}$的取值范围.
解答 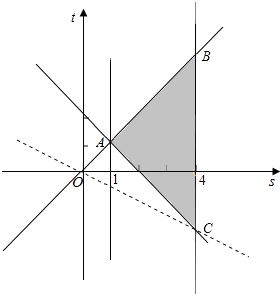 解:由已知条件知f(x)在R上单调递减,且关于原点对称;
解:由已知条件知f(x)在R上单调递减,且关于原点对称;
∴由f(s2-2s)≤-f(2t-t2)得:
s2-2s≥t2-2t;
∴(s-t)(s+t-2)≥0;
以s为横坐标,t为纵坐标建立平面直角坐标系;
不等式组$\left\{\begin{array}{l}{(s-t)(s+t-2)≥0}\\{1≤s≤4}\end{array}\right.$所表示的平面区域,如图所示:
即△ABC及其内部,C(4,-2);
设$\frac{t-2s}{s+t}=z$,整理成:$t=\frac{2+z}{1-z}s$;
${k}_{OC}=-\frac{1}{2},{k}_{AB}=1$;
∴$-\frac{1}{2}≤\frac{2+z}{1-z}≤1$,解得:$-5≤z≤-\frac{1}{2}$;
∴$\frac{t-2s}{s+t}$的取值范围是[$-5,-\frac{1}{2}$].
故选:D.
点评 考查减函数的定义,图象的平移,奇函数的定义,以及二元一次不等式组表示平面区域,线性规划的概念,及其应用,过原点的一次函数的斜率的求解.

 孟建平名校考卷系列答案
孟建平名校考卷系列答案| A. | 1+i | B. | 1-i | C. | 2+i | D. | 2-i |
| A. | (2,-1) | B. | (-2,-4) | C. | (4,2) | D. | (-1,2) |
| A. | $\frac{mk}{2}-1$ | B. | $\frac{mk}{2}$ | C. | $\frac{mk+1}{2}$ | D. | $\frac{mk}{2}+1$ |
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 非充分又非必要条件 |
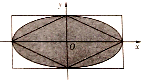 如图,已知矩形长为6,宽为4,在矩形内随机地撒75颗黄豆,数得落在椭圆$\frac{{x}^{2}}{9}$+$\frac{{y}^{2}}{4}$=1外的黄豆数16颗,现随机向椭圆内丢一粒豆子,则豆子落在菱形(菱形顶点为椭圆的顶点)区域内的概率为$\frac{75}{118}$.
如图,已知矩形长为6,宽为4,在矩形内随机地撒75颗黄豆,数得落在椭圆$\frac{{x}^{2}}{9}$+$\frac{{y}^{2}}{4}$=1外的黄豆数16颗,现随机向椭圆内丢一粒豆子,则豆子落在菱形(菱形顶点为椭圆的顶点)区域内的概率为$\frac{75}{118}$.