题目内容
设存在实数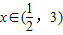 ,使不等式
,使不等式 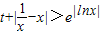 成立,则实数t的取值范围为 .
成立,则实数t的取值范围为 .
【答案】分析:考虑关键点x=1处,分为以下两端:①x∈( ,1]时,t>
,1]时,t> ;②x∈(1,3]时,t≥
;②x∈(1,3]时,t≥ ,综上所述,t>
,综上所述,t> .
.
解答:解:考虑关键点x=1处,分为以下两端:
①x∈( ,1]时,
,1]时,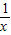 -x≥0,lnx≤0,
-x≥0,lnx≤0,
于是t+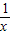 -x>e-lnx,
-x>e-lnx,
即 t>-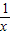 +x+
+x+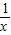 =x>
=x> ,此时t>
,此时t> .
.
②x∈(1,3]时,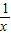 -x<0; lnx>0,
-x<0; lnx>0,
于是t-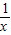 +x>elnx,
+x>elnx,
即 t>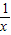 -x+x=
-x+x=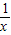
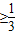 ,此时t≥
,此时t≥ ,
,
综上所述,t> .
.
故答案为:t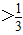 .
.
点评:本题考查不等式的性质和应用,解题时要认真审题,仔细解答,注意分类讨论思想的合理运用.
 ,1]时,t>
,1]时,t> ;②x∈(1,3]时,t≥
;②x∈(1,3]时,t≥ ,综上所述,t>
,综上所述,t> .
.解答:解:考虑关键点x=1处,分为以下两端:
①x∈(
 ,1]时,
,1]时,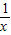 -x≥0,lnx≤0,
-x≥0,lnx≤0,于是t+
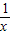 -x>e-lnx,
-x>e-lnx,即 t>-
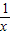 +x+
+x+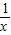 =x>
=x> ,此时t>
,此时t> .
.②x∈(1,3]时,
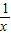 -x<0; lnx>0,
-x<0; lnx>0,于是t-
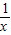 +x>elnx,
+x>elnx,即 t>
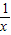 -x+x=
-x+x=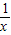
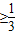 ,此时t≥
,此时t≥ ,
,综上所述,t>
 .
.故答案为:t
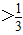 .
.点评:本题考查不等式的性质和应用,解题时要认真审题,仔细解答,注意分类讨论思想的合理运用.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目