题目内容
已知集合A={x|（x-2）[x-（3a+1）＜0]}，B={x|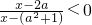
}，若B∩A=B，求实数a的取值范围．
解：由于 a2+1大于等于2a，所以，B=[2a，a2+1]．
若2＜3a+1，A=[2，3a+1]，由A∩B=B，可得 2a＞2，a2+1＜3a+1，且2＜3a+1，解得 1＜a＜3．
若2＞3a+1，A=[3a+1，2]，由A∩B=B，可得 2a＞3a+1，a2+1＜2，且2＞3a+1，这时，a无解．
综上可得，1＜a＜3，故 实数a的取值范围为（1，3）．
分析：先求出 B=[2a，a2+1]，分2＜3a+1和 2＞3a+1两种情况，分别根据A∩B=B求出实数a的取值范围，再取并集即得所求
点评：本题主要考查集合关系中参数的取值范围问题，体现了分类讨论的数学思想，属于基础题．
若2＜3a+1，A=[2，3a+1]，由A∩B=B，可得 2a＞2，a2+1＜3a+1，且2＜3a+1，解得 1＜a＜3．
若2＞3a+1，A=[3a+1，2]，由A∩B=B，可得 2a＞3a+1，a2+1＜2，且2＞3a+1，这时，a无解．
综上可得，1＜a＜3，故 实数a的取值范围为（1，3）．
分析：先求出 B=[2a，a2+1]，分2＜3a+1和 2＞3a+1两种情况，分别根据A∩B=B求出实数a的取值范围，再取并集即得所求
点评：本题主要考查集合关系中参数的取值范围问题，体现了分类讨论的数学思想，属于基础题．
练习册系列答案
怎样学好牛津英语系列答案
相关题目