题目内容
已知函数
，若x0是函数y=f（x）的零点，且0＜x1＜x0，则f（x1）
- A.恒为正值
- B.等于0
- C.恒为负值
- D.不大于0
A
分析：根据指数函数与对数函数的性质可得：为减函数，所以结合题意可得：f（x1）＞f（x0）=0．
解答：根据指数函数与对数函数的性质可得：为减函数，
因为x0是函数y=f（x）的零点，
所以f（x0）=0．
因为0＜x1＜x0，
所以有：f（x1）＞f（x0）=0．
故选A．
点评：本题主要考查函数的单调性与函数的零点．
分析：根据指数函数与对数函数的性质可得：
为减函数，所以结合题意可得：f（x1）＞f（x0）=0．解答：根据指数函数与对数函数的性质可得：
为减函数，因为x0是函数y=f（x）的零点，
所以f（x0）=0．
因为0＜x1＜x0，
所以有：f（x1）＞f（x0）=0．
故选A．
点评：本题主要考查函数的单调性与函数的零点．
练习册系列答案
相关题目
已知函数f（x）=（
）x-log3x，若x0是函数y=f（x）的零点，且0＜x1＜x0，则f（x1）（ ）
| 1 |
| 5 |
| A、恒为正值 | B、等于0 |
| C、恒为负值 | D、不大于0 |
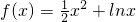
，求c的取值范围．