题目内容
已知函数 .
.
(1)求函数f(x)的最小正周期;
(2)求函数h(x)=f(x)-g(x)的单调递增区间;
(3)当 时,求函数h(x)的最大值与最小值.
时,求函数h(x)的最大值与最小值.
解:(1)
= ,
,
所以周期T= =π
=π
(2)h(x)=f(x)-g(x)= ,
,
由2kπ-π≤2x ≤2kπ,得
≤2kπ,得
∴函数h(x)=f(x)-g(x)的单调递增区间为
(3)由(2)知 ,
,
当 时,
时, ,
,
∴当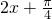 =
= ,即x=0时,
,即x=0时, ,
,
当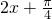 =π,即x=
=π,即x= 时,
时,
∴函数h(x)的最大值与最小值分别为 ,-
,-
分析:(1)先利用两角和差的余弦公式和二倍角公式,将函数f(x)化为y=Acos(ωx+φ)型函数,再利用周期计算公式得函数的最小正周期;
(2)先利用两角和的余弦公式将函数h(x)化为y=Acos(ωx+φ)型函数,再将内层函数看作整体放到余弦曲线的增区间上,即可解得函数的单调增区间;
(3)先求内层函数的值域,再利用余弦函数的图象和性质求整个函数的值域,从而得其最值
点评:本题主要考查了三角变换公式的运用,y=Acos(ωx+φ)型函数的图象和性质,整体代换的思想方法

=
 ,
,所以周期T=
 =π
=π(2)h(x)=f(x)-g(x)=
 ,
,由2kπ-π≤2x
 ≤2kπ,得
≤2kπ,得
∴函数h(x)=f(x)-g(x)的单调递增区间为

(3)由(2)知
 ,
,当
 时,
时, ,
,∴当
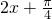 =
= ,即x=0时,
,即x=0时, ,
,当
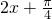 =π,即x=
=π,即x= 时,
时,
∴函数h(x)的最大值与最小值分别为
 ,-
,-
分析:(1)先利用两角和差的余弦公式和二倍角公式,将函数f(x)化为y=Acos(ωx+φ)型函数,再利用周期计算公式得函数的最小正周期;
(2)先利用两角和的余弦公式将函数h(x)化为y=Acos(ωx+φ)型函数,再将内层函数看作整体放到余弦曲线的增区间上,即可解得函数的单调增区间;
(3)先求内层函数的值域,再利用余弦函数的图象和性质求整个函数的值域,从而得其最值
点评:本题主要考查了三角变换公式的运用,y=Acos(ωx+φ)型函数的图象和性质,整体代换的思想方法

练习册系列答案
相关题目





 ,如果满足;对任意
,如果满足;对任意 ,存在常数
,存在常数 ,都有
,都有 成立,则称
成立,则称 ,
,
 时,求函数
时,求函数 上的值域,并判断函数
上的值域,并判断函数 上是以3为上界函数值,求实数
上是以3为上界函数值,求实数 的取值范围;
的取值范围; ,求函数
,求函数 在
在 上的上界T的取值范围。
上的上界T的取值范围。 .
. 上的函数值的取值范围.
上的函数值的取值范围. .
. 上的函数值的取值范围.
上的函数值的取值范围.