题目内容
10.已知sinα,sinβ是方程8x2-6kx+2k+1=0的两根,且α.β终边互相垂直,则k=-$\frac{10}{9}$.分析 sinα,sinβ是方程8x2-6kx+2k+1=0的两根,可得:sinα+sinβ=$\frac{3k}{4}$,sinα•sinβ=$\frac{2k+1}{8}$.又α.β终边互相垂直,不妨设$β=α+2kπ+\frac{π}{2}$.可得sinβ=cosα.于是sinα+cosα=$\frac{3k}{4}$,sinα•cosα=$\frac{2k+1}{8}$.利用同角三角函数基本关系式即可得出.
解答 解:∵sinα,sinβ是方程8x2-6kx+2k+1=0的两根,
∴sinα+sinβ=$\frac{3k}{4}$,sinα•sinβ=$\frac{2k+1}{8}$.
又α.β终边互相垂直,
不妨设$β=α+2kπ+\frac{π}{2}$.
∴sinβ=cosα.
∴sinα+cosα=$\frac{3k}{4}$≤$\sqrt{2}$,sinα•cosα=$\frac{2k+1}{8}$.
∴$\frac{9{k}^{2}}{16}$=1+2×$\frac{2k+1}{8}$,
化为9k2-8k-20=0,
则k=2(舍去)或k=-$\frac{10}{9}$.
故答案为:-$\frac{10}{9}$.
点评 本题考查了终边相同的角、同角三角函数基本关系式、一元二次方程的根与系数的关系,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案
相关题目
2.已知x,y∈R,a>1且ax+(a+1)y≥a-y+(a+1)-x,则x与y满足 ( )
| A. | x+y≥0 | B. | x+y≤0 | C. | x-y≤0 | D. | x-y≥0 |
15.2≤|x|+|y|≤3,则x2+y2-2x的取值范围是( )
| A. | [$\frac{\sqrt{2}-2}{2}$,3] | B. | [$\frac{\sqrt{2}}{2}$,4] | C. | [-$\frac{1}{2}$,15] | D. | [$\frac{1}{2}$,16] |
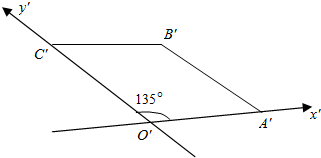 在直观图如图中,四边形O′A′B′C′为菱形且边长为2cm,则在xOy坐标系中原四边形OABC为矩形(填形状),面积为8cm2.
在直观图如图中,四边形O′A′B′C′为菱形且边长为2cm,则在xOy坐标系中原四边形OABC为矩形(填形状),面积为8cm2.