题目内容
已知双曲线S的两个焦点F1、F2在x轴上,它的两条渐近线分别为l1、l2,y=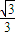 x是其中的一条渐近线的方程,两条直线X=±
x是其中的一条渐近线的方程,两条直线X=± 是双曲线S的准线.
是双曲线S的准线.(I)设A、B分别为l1、l2上的动点,且2|
 |=5
|=5 ,求线段AB的中点M的轨迹方程:
,求线段AB的中点M的轨迹方程:(II)已知O是原点,经过点N(0,1)是否存在直线l,使l与双曲线S交于P,E且△POE是以PE为斜边的直角三角形?若存在,求出直线l的方程;若不存在,请说明理由.
【答案】分析:先利用已知条件求出双曲线S的标准方程;
(I)设出M(x,y),A(x1,y1),B(x2,y2),根据中点坐标公式得x1+x2=2x,y1+y2=2y;再根据已知得y= x是l1,l2的方程,A,B,分别为l1,l2上的点.以及弦长公式和2|
x是l1,l2的方程,A,B,分别为l1,l2上的点.以及弦长公式和2| |=5
|=5 ,即得答案:
,即得答案:
(II)先设出直线l的方程,把直线方程与双曲线方程联立,得到P,E坐标与直线斜率之间的等量关系;再结合△POE是以PE为斜边的直角三角形对应的结论 =0.即可求出最终结论.(注意对直线方程分斜率存在和不存在两种情况来讨论)
=0.即可求出最终结论.(注意对直线方程分斜率存在和不存在两种情况来讨论)
解答:解:根据题意设双曲线S的方程为 ,
,
根据已知,得 ,解方程组,得
,解方程组,得 ,
,
∴双曲线S的方程为 .
.
(I)设M(x,y),A(x1,y1),B(x2,y2),则 ,
,
即x1+x2=2x,y1+y2=2y,
∵ ,
,
∴ ,
,
即 =10.
=10.
由已知得y= x是l1,l2的方程,A,B,分别为l1,l2上的点.
x是l1,l2的方程,A,B,分别为l1,l2上的点.
所以(y1+y2)2= (x1-x2)2.即(x2-x1)2=3(y2+y1)2.
(x1-x2)2.即(x2-x1)2=3(y2+y1)2.
(y2-y1)2= .
.
∴ =
= =10.
=10.
∴3×(2y)2+ (2x)2=100.即
(2x)2=100.即 .
.
所以线段AB的中点M的轨迹方程为: .
.
(II)∵经过点N(0,1),斜率不存在的直线是x=0,它与曲线S不相交,
∴经过点N(0,1)斜率不存在的直线不符合要求.
当经过点N(0,1)的直线斜率存在时,设方程为y=kx+1.
假设它满足要求,根据已知设P(x3,kx3+1),E(x4,kx4+1)
∵△POE是以PE为斜边的指直角三角形
∴ =0.即x3x4+(kx3+1)(kx4+1)=0.
=0.即x3x4+(kx3+1)(kx4+1)=0.
∴(1+k2)x3x4+k(x3+x4)+1=0.
由 得(1-3k2)x2-6kx-6=0.
得(1-3k2)x2-6kx-6=0.
∴x3+x4= ,x3•x4=
,x3•x4= .
.
∴(1+k2) =1.化简得:3k2+5=0,此方程无实数根.
=1.化简得:3k2+5=0,此方程无实数根.
所以经过点N(0,1)斜率存在的直线l也不满足要求.
综上可得:满足要求的直线l不存在.
点评:本题是一道综合性很强的好题.涉及到的知识点有:双曲线标准方程的求法,轨迹方程的求法,两点间的距离公式,以及韦达定理等,是对知识的综合考查,要想在这种类型题目上得分,需要有比较扎实的基本功.
(I)设出M(x,y),A(x1,y1),B(x2,y2),根据中点坐标公式得x1+x2=2x,y1+y2=2y;再根据已知得y=
 x是l1,l2的方程,A,B,分别为l1,l2上的点.以及弦长公式和2|
x是l1,l2的方程,A,B,分别为l1,l2上的点.以及弦长公式和2| |=5
|=5 ,即得答案:
,即得答案:(II)先设出直线l的方程,把直线方程与双曲线方程联立,得到P,E坐标与直线斜率之间的等量关系;再结合△POE是以PE为斜边的直角三角形对应的结论
 =0.即可求出最终结论.(注意对直线方程分斜率存在和不存在两种情况来讨论)
=0.即可求出最终结论.(注意对直线方程分斜率存在和不存在两种情况来讨论)解答:解:根据题意设双曲线S的方程为
 ,
,根据已知,得
 ,解方程组,得
,解方程组,得 ,
,∴双曲线S的方程为
 .
.(I)设M(x,y),A(x1,y1),B(x2,y2),则
 ,
,即x1+x2=2x,y1+y2=2y,
∵
 ,
,∴
 ,
,即
 =10.
=10.由已知得y=
 x是l1,l2的方程,A,B,分别为l1,l2上的点.
x是l1,l2的方程,A,B,分别为l1,l2上的点.所以(y1+y2)2=
 (x1-x2)2.即(x2-x1)2=3(y2+y1)2.
(x1-x2)2.即(x2-x1)2=3(y2+y1)2.(y2-y1)2=
 .
.∴
 =
= =10.
=10.∴3×(2y)2+
 (2x)2=100.即
(2x)2=100.即 .
.所以线段AB的中点M的轨迹方程为:
 .
.(II)∵经过点N(0,1),斜率不存在的直线是x=0,它与曲线S不相交,
∴经过点N(0,1)斜率不存在的直线不符合要求.
当经过点N(0,1)的直线斜率存在时,设方程为y=kx+1.
假设它满足要求,根据已知设P(x3,kx3+1),E(x4,kx4+1)
∵△POE是以PE为斜边的指直角三角形
∴
 =0.即x3x4+(kx3+1)(kx4+1)=0.
=0.即x3x4+(kx3+1)(kx4+1)=0.∴(1+k2)x3x4+k(x3+x4)+1=0.
由
 得(1-3k2)x2-6kx-6=0.
得(1-3k2)x2-6kx-6=0.∴x3+x4=
 ,x3•x4=
,x3•x4= .
.∴(1+k2)
 =1.化简得:3k2+5=0,此方程无实数根.
=1.化简得:3k2+5=0,此方程无实数根.所以经过点N(0,1)斜率存在的直线l也不满足要求.
综上可得:满足要求的直线l不存在.
点评:本题是一道综合性很强的好题.涉及到的知识点有:双曲线标准方程的求法,轨迹方程的求法,两点间的距离公式,以及韦达定理等,是对知识的综合考查,要想在这种类型题目上得分,需要有比较扎实的基本功.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
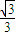 x是其中的一条渐近线的方程,两条直线X=±
x是其中的一条渐近线的方程,两条直线X=± 是双曲线S的准线.
是双曲线S的准线. |=5
|=5 ,求线段AB的中点M的轨迹方程:
,求线段AB的中点M的轨迹方程: