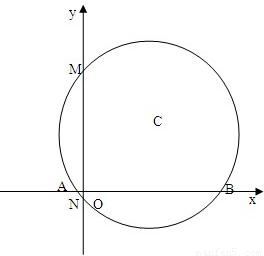
题目内容
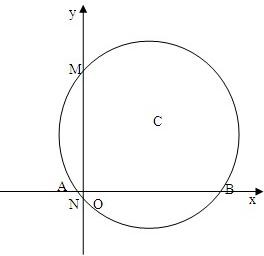 已知圆C满足:
已知圆C满足:(1)截y轴所得弦MN长为4;
(2)被x轴分成两段圆弧,其弧 长之比为3:1,且圆心在直线y=x上,求圆C的方程.(为方便学生解答,做了一种情形的辅助图形)
分析:设出圆的方程,圆心为(a,b),半径为r,根据垂径定理及勾股定理得到r2=4+a2,根据圆C被x轴分成的两点圆弧,弧长之比为3:1,得到角ACB等于90°,得到圆的半径r等于
|b|,又根据圆心在直线y=x上,把圆心坐标代入y=x中得到a=b,
把得到的三个等式联立即可求出a,b及r的值,进而得到圆C的圆心坐标及半径,根据圆心和半径写出圆的方程即可.
| 2 |
把得到的三个等式联立即可求出a,b及r的值,进而得到圆C的圆心坐标及半径,根据圆心和半径写出圆的方程即可.
解答:解:设圆的方程是(x-a)2+(y-b)2=r2,圆心是(a,b),半径是r,
∵圆截y轴所得弦长为4,
∴r2=4+a2.
∵被x轴分成两段圆弧,其弧长之比为3:1,
∴r=
|b|.
∵圆心(a,b)在直线y=x上,
∴b=a.
∴
,
解得:a=b=2,r=2
或者a=b=-2,r=2
,
所以圆的方程:(x-2)2+(y-2)2=8或者(x+2)2+(y+2)2=8.
∵圆截y轴所得弦长为4,
∴r2=4+a2.
∵被x轴分成两段圆弧,其弧长之比为3:1,
∴r=
| 2 |
∵圆心(a,b)在直线y=x上,
∴b=a.
∴
|
解得:a=b=2,r=2
| 2 |
| 2 |
所以圆的方程:(x-2)2+(y-2)2=8或者(x+2)2+(y+2)2=8.
点评:此题考查学生灵活运用韦达定理及勾股定理化简求值,掌握圆中的弧之比所对的圆心角之比的性质,是一道多知识的综合题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

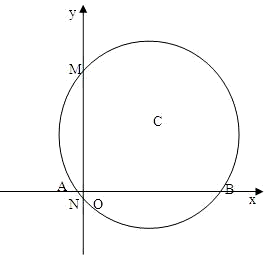 已知圆C满足:
已知圆C满足: