Question

（2009•红桥区二模）已知圆C：（x+1）²+y²=8，定点A（1，0），M为圆上一动点，点P在AM上，且满足

AP

=

PM

，过点P且与AM垂直的直线交CM于N
（Ⅰ）求点N的轨迹E的方程：
（Ⅱ）设⊙O是以AC为直径的圆，直线l：y=kx+m与⊙O相切，并与椭圆交于不同的两点G、H，当

OG

•

OH

=λ，且满足

2

3

≤λ≤

3

4

时，求△GOH面积S的取值范围．

Answer 1

分析：（I）如图所示．由于满足

AP

=

PM

，过点P且与AM垂直的直线交CM于N，可知：PN垂直平分AM，连接AN．可得|NC|+|NA|=|CM|=2

2

＞|AC|=2，由椭圆的定义可知：点N的轨迹E是椭圆，
（II）利用直线与⊙O相切的性质可得k与m的关系，把直线GH与椭圆方程联立得到△＞0及根与系数的关系，再利用弦长公式和三角形的面积公式和已知λ的取值范围即可得到k的取值范围，进而得到三角形的面积的取值范围．

解答：解：（I）如图所示．由于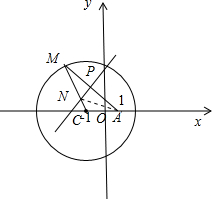满足

AP

=

PM

，过点P且与AM垂直的直线交CM于N，
∴PN垂直平分AM，连接AN．
则|AN|=|NM|，
∴|NC|+|NA|=|CM|=2

2

＞|AC|=2，
由椭圆的定义可知：点N的轨迹E是以点C（-1，0），A（1，0）为焦点，2

2

为长轴长的椭圆，
∴b²=a²-c²=1．
其方程为

x2

2

+y2=1；
（II）如图所示．以AC为直径的圆的方程为：x²+y²=1．
设直线GH与⊙O相切于点T，则|OT|=1，∴

|m|

1+k2

=1，化为m²=k²+1
设G（x₁，y₁），H（x₂，y₂）．联立

y=kx+m x2 2 +y2=1

，化为（1+2k²）x²+4kmx+2m²-2=0．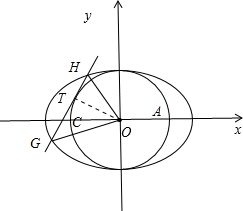
则△=16k²m²-8（1+2k²）（m²-1）＞0，即k²＞0．
∴x1+x2=-

4km

1+2k2

，x1x2=

2m2-2

1+2k2

．
∴|GH|=

1+k2

|x1-x2|=

1+k2

•

(x1+x2)2-4x1x2

=

2 2 1+k2

1+2k2

•

1+2k2-m2

=

2 2k2(1+k2)

1+2k2

．
∴S=S_△OGH=

1

2

|GH|•|OT|=

2k2(1+k2)

1+2k2

=

2k2+2k4 1+4k2+4k4

．
又λ=

OG

•

OH

=x₁x₂+y₁y₂=x₁x₂+（kx₁+m）（kx₂+m）=(1+k2)x1x2+mk(x1+x2)+m2=

(1+k2)(2m2-2)

1+2k2

-

4k2m2

1+2k2

+m²=

3m2-2k2-2

1+2k2

=

1+k2

1+2k2

，
∵

2

3

≤λ≤

3

4

，
∴

2

3

≤

1+k2

1+2k2

≤

3

4

．
解得

1

2

≤k2≤1．
令k²=t＞0，则S=

2t+2t2 1+4t+4t2

=

1 2 - 1 2(1+2t)2

．
由

1

2

≤t≤1，得2≤1+2t≤3，∴

1

18

≤

1

2(1+2t)2

≤

1

8

，∴

3

8

≤

1

2

-

1

2(1+2t)2

≤

4

9

．
∴

6

4

≤S≤

2

3

．

点评：本题综合考查了椭圆与圆的标准方程及其性质、直线与圆相切的性质、直线与椭圆相交问题转化为方程联立得到△＞0即根与系数的关系、弦长公式、三角形的面积计算公式、二次函数的单调性等基础知识与基本方法，考查了计算能力、推理能力和解决复杂问题的能力．