题目内容
已知椭圆 经过点
经过点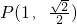 ,且两焦点与短轴的一个端点构成等腰直角三角形.
,且两焦点与短轴的一个端点构成等腰直角三角形.
(1)求椭圆的方程;
(2)动直线 交椭圆C于A、B两点,试问:在坐标平面上是否存在一个定点T,使得以AB为直径的圆恒过点T.若存在,求出点T的坐标;若不存在,请说明理由.
交椭圆C于A、B两点,试问:在坐标平面上是否存在一个定点T,使得以AB为直径的圆恒过点T.若存在,求出点T的坐标;若不存在,请说明理由.
解:(1)∵椭圆 的两焦点与短轴的一个端点的连线构成等腰直角三角形,
的两焦点与短轴的一个端点的连线构成等腰直角三角形,
∴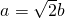 ∴
∴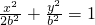
又∵椭圆经过点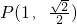 ,代入可得b=1,
,代入可得b=1,
∴ ,故所求椭圆方程为
,故所求椭圆方程为 (3分)
(3分)
(2)首先求出动直线过(0, )点.(5分)
)点.(5分)
当L与x轴平行时,以AB为直径的圆的方程: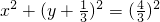
当L与y轴平行时,以AB为直径的圆的方程:x2+y2=1
由
即两圆相切于点(0,1),因此,所求的点T如果存在,只能是(0,1).事实上,点T(0,1)就是所求的点.(7分)
证明如下:
当直线L垂直于x轴时,以AB为直径的圆过点T(0,1)
若直线L不垂直于x轴,可设直线L: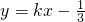
由
记点A(x1,y1)、 (9分)
(9分)
 =
= =
=
所以TA⊥TB,即以AB为直径的圆恒过点T(0,1)
所以在坐标平面上存在一个定点T(0,1)满足条件.(12分)
分析:(1)由题设知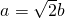 ,所以
,所以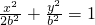 ,椭圆经过点
,椭圆经过点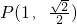 ,代入可得b=1,
,代入可得b=1, ,由此可知所求椭圆方程为
,由此可知所求椭圆方程为
(2)首先求出动直线过(0, )点.当L与x轴平行时,以AB为直径的圆的方程:
)点.当L与x轴平行时,以AB为直径的圆的方程: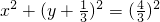 ;当L与y轴平行时,以AB为直径的圆的方程:x2+y2=1.由
;当L与y轴平行时,以AB为直径的圆的方程:x2+y2=1.由 .由此入手可求出点T的坐标.
.由此入手可求出点T的坐标.
点评:本题考查圆锥曲线的性质和综合运用,解题时要认真审题,仔细求解.
 的两焦点与短轴的一个端点的连线构成等腰直角三角形,
的两焦点与短轴的一个端点的连线构成等腰直角三角形,∴
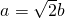 ∴
∴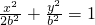
又∵椭圆经过点
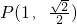 ,代入可得b=1,
,代入可得b=1,∴
 ,故所求椭圆方程为
,故所求椭圆方程为 (3分)
(3分)(2)首先求出动直线过(0,
 )点.(5分)
)点.(5分)当L与x轴平行时,以AB为直径的圆的方程:
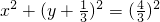
当L与y轴平行时,以AB为直径的圆的方程:x2+y2=1
由

即两圆相切于点(0,1),因此,所求的点T如果存在,只能是(0,1).事实上,点T(0,1)就是所求的点.(7分)
证明如下:
当直线L垂直于x轴时,以AB为直径的圆过点T(0,1)
若直线L不垂直于x轴,可设直线L:
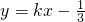
由

记点A(x1,y1)、
 (9分)
(9分)
 =
= =
=
所以TA⊥TB,即以AB为直径的圆恒过点T(0,1)
所以在坐标平面上存在一个定点T(0,1)满足条件.(12分)
分析:(1)由题设知
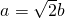 ,所以
,所以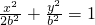 ,椭圆经过点
,椭圆经过点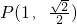 ,代入可得b=1,
,代入可得b=1, ,由此可知所求椭圆方程为
,由此可知所求椭圆方程为
(2)首先求出动直线过(0,
 )点.当L与x轴平行时,以AB为直径的圆的方程:
)点.当L与x轴平行时,以AB为直径的圆的方程: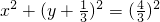 ;当L与y轴平行时,以AB为直径的圆的方程:x2+y2=1.由
;当L与y轴平行时,以AB为直径的圆的方程:x2+y2=1.由 .由此入手可求出点T的坐标.
.由此入手可求出点T的坐标.点评:本题考查圆锥曲线的性质和综合运用,解题时要认真审题,仔细求解.

练习册系列答案
相关题目
 经过点
经过点 ,且两焦点与短轴的一个端点构成等腰直角三角形.
,且两焦点与短轴的一个端点构成等腰直角三角形. 交椭圆
交椭圆 于
于 、
、 两点,试问:在坐标平面上是否存在一个定点
两点,试问:在坐标平面上是否存在一个定点 ,使得以
,使得以 为直径的圆恒过点
为直径的圆恒过点 经过点
经过点 ,且两焦点与短轴的一个端点的连线构成等腰直角三角形.
,且两焦点与短轴的一个端点的连线构成等腰直角三角形. 交椭圆C于A、B两点,试问:在坐标平面上是否存在一个定点T,使得以AB为直径的圆恒过点T。若存在,求出点T的坐标;若不存在,请说明理由.
交椭圆C于A、B两点,试问:在坐标平面上是否存在一个定点T,使得以AB为直径的圆恒过点T。若存在,求出点T的坐标;若不存在,请说明理由. 经过点
经过点 ,且两焦点与短轴的一个端点的连线构成等腰直角三角形.(1)求椭圆的方程;
,且两焦点与短轴的一个端点的连线构成等腰直角三角形.(1)求椭圆的方程; 交椭圆C于A、B两点,试问:在坐标平面上是否存在一个定点T,使得以AB为直径的圆恒过点T。若存在,求出点T的坐标;若不存在,请说明理由.
交椭圆C于A、B两点,试问:在坐标平面上是否存在一个定点T,使得以AB为直径的圆恒过点T。若存在,求出点T的坐标;若不存在,请说明理由. 经过点
经过点 ,且两焦点与短轴一端点构成等腰直角三角形。
,且两焦点与短轴一端点构成等腰直角三角形。 交椭圆C于A、B两点,试问:在坐标平面上是否存在一个定点T,使得以AB为直径的圆恒过点T。若存在,求出点T的坐标;若不存在,请说明理由。
交椭圆C于A、B两点,试问:在坐标平面上是否存在一个定点T,使得以AB为直径的圆恒过点T。若存在,求出点T的坐标;若不存在,请说明理由。