题目内容
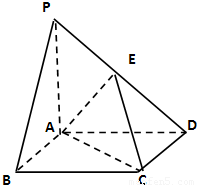
如图，ABCD为正方形，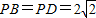
，且PA=AD=2．（1）求证：PA⊥平面ABCD；
（2）若E是线段PD的中点，求三棱锥C-ADE的体积．
【答案】分析：（1）根据勾股定理可证得PA与AB，AD均垂直，进而根据线面垂直的判定定理得到答案．
（2）三棱锥C-ADE的体积可看作是三棱锥E-ACD的体积，由E是线段PD的中点，则E到底面的距离为PA的一半，求出棱锥的底面面积和高后，代入棱锥体积公式，可得答案．
解答：证明：（1）∵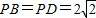
，且PA=AD=2．
∴在△PAD中，PD2=PA2+AD2，
则∠PAD=90°，即PA⊥AD
同理PA⊥AB
又∵AD∩AB=A，AB，AD?平面ABCD
∴PA⊥平面ABCD；
解：（2）∵E是线段PD的中点，
∴E到平面ABCD的距离h=
PA=1
∵S△ACD=
×2×2=2
∴三棱锥C-ADE的体积VC-ADE=VE-ACD=
•S△ACD•h=
点评：本题考查的知识点是直线与平面垂直的判定，棱锥的体积，其中熟练掌握线面垂直的判定定理是解答的关键．
（2）三棱锥C-ADE的体积可看作是三棱锥E-ACD的体积，由E是线段PD的中点，则E到底面的距离为PA的一半，求出棱锥的底面面积和高后，代入棱锥体积公式，可得答案．
解答：证明：（1）∵
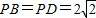，且PA=AD=2．∴在△PAD中，PD2=PA2+AD2，
则∠PAD=90°，即PA⊥AD
同理PA⊥AB
又∵AD∩AB=A，AB，AD?平面ABCD
∴PA⊥平面ABCD；
解：（2）∵E是线段PD的中点，
∴E到平面ABCD的距离h=
PA=1∵S△ACD=
×2×2=2∴三棱锥C-ADE的体积VC-ADE=VE-ACD=
•S△ACD•h=点评：本题考查的知识点是直线与平面垂直的判定，棱锥的体积，其中熟练掌握线面垂直的判定定理是解答的关键．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
（下列两道题任选做一道，若两道都做，则以第一道计分）
如图所示为某风景区设计建造的一个休闲广场，广场的中间造型的平面图是由两个相同的矩形ABCD和EFGH构成对称的十字形区域，十字形区域面积为2000m2，计划在正方方形MNPQ上建一座“观景花坛”，造价为每平方4100元，在四个相同的矩形上（图中阴影部分）铺石材地坪，价格为每平方110元，再在四个空角（如△DQH等）上铺草坪，价格为每平方80元．设AD长为xm，DQ长为ym．
如图所示为某风景区设计建造的一个休闲广场，广场的中间造型的平面图是由两个相同的矩形ABCD和EFGH构成对称的十字形区域，十字形区域面积为2000m2，计划在正方方形MNPQ上建一座“观景花坛”，造价为每平方4100元，在四个相同的矩形上（图中阴影部分）铺石材地坪，价格为每平方110元，再在四个空角（如△DQH等）上铺草坪，价格为每平方80元．设AD长为xm，DQ长为ym．
