题目内容
已知函数 的图象如图所示,则
的图象如图所示,则 满足的关系是( )
满足的关系是( )
A. | B.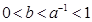 |
C. | D. |
A
解析试题分析: ∵函数f(x)=loga(2x+b-1)是增函数且随着x增大,2x+b-1增大,f(x)也增大.
∴a>1,∴0< <1,∵当x=0时,f(0)=logab<0,∴0<b<1.又∵f(0)=logab>-1=loga
<1,∵当x=0时,f(0)=logab<0,∴0<b<1.又∵f(0)=logab>-1=loga ,
,
∴b> ,∴0<a-1<b<1,故结合选项可知选A.
,∴0<a-1<b<1,故结合选项可知选A.
考点:本题主要考查了对数函数的图象性质,考查学生的识图能力.考查学生的数形结合能力和等价转化思想.
点评:利用对数函数和函数图象平移的方法列出关于a,b的不等关系是解决本题的关键.利用好图形中的标注的(0,-1)点.利用复合函数思想进行单调性的判断,进而判断出底数与1的大小关系.

练习册系列答案
相关题目
已知函数 ,正实数
,正实数 满足
满足 ,且
,且 ,若
,若 在区间
在区间 上的最大值为2,则
上的最大值为2,则 的值为( )
的值为( )
A. | B. | C. | D. |
若函数
A. | B. |
C. | D. |
设f(x)是R上的奇函数,且当x>0时,f(x)=x(1+ ),则当x<0时,f(x)=( )
),则当x<0时,f(x)=( )
A.-x(1+ ) ) | B.x(1+ ) ) | C.-x(1- ) ) | D. x(1- ) ) |
设函数 上单调递增,则
上单调递增,则 的大小关系为( )
的大小关系为( )
A. | B. |
C. | D.不确定 |
 在区间
在区间 上是增函数,实数
上是增函数,实数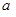 组成集合
组成集合 ;设关于
;设关于 的方程
的方程 的两个非零实根
的两个非零实根 实数
实数 使得不等式
使得不等式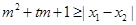 使得对任意
使得对任意 及
及 恒成立,则
恒成立,则



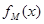 的定义域为R,且定义如下:
的定义域为R,且定义如下: (其中M是实数集R的非空真子集),在实数集R上有两个非空真子集A、B满足
(其中M是实数集R的非空真子集),在实数集R上有两个非空真子集A、B满足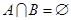 ,则函数
,则函数 的值域为
的值域为 




 )
)  ,定义运算
,定义运算 ,其中
,其中 是常数,等式右边的运算是通常的加法和乘法运算.已知
是常数,等式右边的运算是通常的加法和乘法运算.已知 ,并且有一个非零常数
,并且有一个非零常数 ,使得对任意实数
,使得对任意实数 ,都有
,都有 ,则
,则


