题目内容
设函数 ,它们的图象在x轴上的公共点处有公切线,则当x>1时,f(x)与g(x)的大小关系是
,它们的图象在x轴上的公共点处有公切线,则当x>1时,f(x)与g(x)的大小关系是
- A.f(x)>g(x)
- B.f(x)<g(x)
- C.f(x)=g(x)
- D.f(x)>g(x)与g(x)的大小不确定
B
分析:f(x)与x轴的交点(1,0)在g(x)上,所以a+b=0,在此点有公切线,即此点导数相等,可求出a与b的值,令h(x)=f(x)-g(x),然后利用导数研究该函数在(1,+∞)上的单调性,从而得到正确选项.
解答:f(x)与x轴的交点′(1,0)在g(x)上,
所以a+b=0,在此点有公切线,即此点导数相等,
f′(x)= ,g′(x)=a-
,g′(x)=a-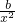 ,
,
以上两式在x=1时相等,即1=a-b,
又因为a+b=0,
所以a= ,b=-
,b=- ,
,
即g(x)= -
- ,f(x)=lnx,
,f(x)=lnx,
定义域{x|x>0},
令h(x)=f(x)-g(x)=lnx- +
+ ,
,
对x求导,得h′(x)= -
- -
-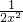 =
= =-
=-
∵x>1
∴h′(x)≤0
∴h(x)在(1,+∞)单调递减,即h(x)<0
∴f(x)<g(x)
故选B.
点评:本题主要考查了利用导数研究曲线上某点切线方程,以及函数的基本性质,同时考查分析问题的能力,属于中档题.
分析:f(x)与x轴的交点(1,0)在g(x)上,所以a+b=0,在此点有公切线,即此点导数相等,可求出a与b的值,令h(x)=f(x)-g(x),然后利用导数研究该函数在(1,+∞)上的单调性,从而得到正确选项.
解答:f(x)与x轴的交点′(1,0)在g(x)上,
所以a+b=0,在此点有公切线,即此点导数相等,
f′(x)=
 ,g′(x)=a-
,g′(x)=a-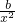 ,
,以上两式在x=1时相等,即1=a-b,
又因为a+b=0,
所以a=
 ,b=-
,b=- ,
,即g(x)=
 -
- ,f(x)=lnx,
,f(x)=lnx,定义域{x|x>0},
令h(x)=f(x)-g(x)=lnx-
 +
+ ,
,对x求导,得h′(x)=
 -
- -
-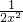 =
= =-
=-
∵x>1
∴h′(x)≤0
∴h(x)在(1,+∞)单调递减,即h(x)<0
∴f(x)<g(x)
故选B.
点评:本题主要考查了利用导数研究曲线上某点切线方程,以及函数的基本性质,同时考查分析问题的能力,属于中档题.

练习册系列答案
相关题目
 ,它们的图象在
,它们的图象在 轴上的公共点处有公切线,则当
轴上的公共点处有公切线,则当 时,
时, 与
与 的大小关系是( )
的大小关系是( ) B.
B.
 D.
D. ,它们的图象在x轴上的公共点处有公切线,则当x>1时,f(x)与g(x)的大小关系是( )
,它们的图象在x轴上的公共点处有公切线,则当x>1时,f(x)与g(x)的大小关系是( ) ,它们的图象在x轴上的公共点处有公切线,则当x>1时,f(x)与g(x)的大小关系是( )
,它们的图象在x轴上的公共点处有公切线,则当x>1时,f(x)与g(x)的大小关系是( )