题目内容
【题目】已知等差数列![]() 满足
满足![]() ,
, ![]()
(I)求数列![]() 的通项公式;
的通项公式;
(II)求数列![]() 的前n项和.
的前n项和.
【答案】(1)![]() (2)
(2)![]()
【解析】试题分析:(1)设等差数列![]() 的公差为
的公差为![]() ,首项为
,首项为![]() , 由
, 由![]() 可列关于
可列关于![]() 、
、![]() 的方程,解得
的方程,解得![]() 、
、![]() 的值即可得结果;(2)
的值即可得结果;(2)![]() ,利用“错位相减法”与等比数列的前
,利用“错位相减法”与等比数列的前![]() 项和公式即可得结果.
项和公式即可得结果.
试题解析:(I)设等差数列![]() 的公差为d,由已知条件可得
的公差为d,由已知条件可得![]()
解得![]() 故数列
故数列![]() 的通项公式为
的通项公式为![]()
(II)设数列![]() ,即
,即![]() ,
,
![]() 所以,当
所以,当![]() 时,
时,
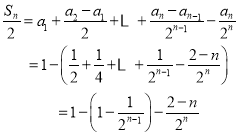
所以![]() 综上,数列
综上,数列![]()
【易错点晴】本题主要考等差数列的通项公式、等比数列的求和公式及“错位相减法”求数列的和,属于中档题. “错位相减法”求数列的和是重点也是难点,利用“错位相减法”求数列的和应注意以下几点:①掌握运用“错位相减法”求数列的和的条件(一个等差数列与一个等比数列的积);②相减时注意最后一项 的符号;③求和时注意项数别出错;④最后结果一定不能忘记等式两边同时除以![]() .
.

练习册系列答案
相关题目