题目内容
一质点从原点出发,第1次移动到点(1,0 ),每次都从到达点出发,第2次移动到点(1,2),第3次移动到点(-2,2),第4次移动到点(-2,-2),第5次移动到点(3,-2)第6次移动到点(3,4),第7次移动到点(-4,4),第8次移动到点(-4,-4),第9次移动到点(5,-4),第10次移动到点(5,6),…,依此类推,到2012次移动前,此质点到达位置的坐标是
(-1006,1006)
(-1006,1006)
.分析:根据已知中前10次移动后点的坐标,分析出移动n次后,点的横坐标的变化规律及纵坐标的变化规律,进而根据到2012次移动前,此质点共移动了2011次,代入可得答案.
解答:解:根据已知中前10移动后点的坐标:
第1次移动到点(1,0 ),第2次移动到点(1,2),
第3次移动到点(-2,2),第4次移动到点(-2,-2),
第5次移动到点(3,-2),第6次移动到点(3,4),
第7次移动到点(-4,4),第8次移动到点(-4,-4),
第9次移动到点(5,-4),第10次移动到点(5,6),
…,
可得移动奇数次后点的横坐标为(-1)
•
点的纵坐标为
-(-1)
•
2012次移动前,此质点共移动了2011次,
到达位置的横坐标是:(-1)
•
=-1006
到达位置的纵坐标是:
-(-1)
•
=
+
=1006
即此质点到达位置的坐标是(-1006,1006)
故答案为:(-1006,1006)
第1次移动到点(1,0 ),第2次移动到点(1,2),
第3次移动到点(-2,2),第4次移动到点(-2,-2),
第5次移动到点(3,-2),第6次移动到点(3,4),
第7次移动到点(-4,4),第8次移动到点(-4,-4),
第9次移动到点(5,-4),第10次移动到点(5,6),
…,
可得移动奇数次后点的横坐标为(-1)
| n-1 |
| 2 |
| n+1 |
| 2 |
点的纵坐标为
| 1 |
| 2 |
| n-1 |
| 2 |
| n |
| 2 |
2012次移动前,此质点共移动了2011次,
到达位置的横坐标是:(-1)
| 2011-1 |
| 2 |
| 2011+1 |
| 2 |
到达位置的纵坐标是:
| 1 |
| 2 |
| n-1 |
| 2 |
| n |
| 2 |
| 1 |
| 2 |
| 2011 |
| 2 |
即此质点到达位置的坐标是(-1006,1006)
故答案为:(-1006,1006)
点评:本题考查的知识点是归纳推理,其中根据前10次移动质点坐标的变化情况,分析出变化的规律是解答的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目

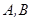 的坐标分别为
的坐标分别为 ,一质点
,一质点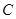 从原点出发,始终沿
从原点出发,始终沿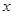 轴的正方向运动,已知第1分钟内,质点
轴的正方向运动,已知第1分钟内,质点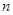 分钟内质点运动了
分钟内质点运动了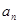 个单位,此时质点的位置为
个单位,此时质点的位置为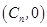 .
.
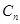 的表达式;
的表达式;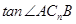 取得最大,最大值为多少?
取得最大,最大值为多少?