Question

（本小题满分12分）如图，定点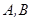的坐标分别为，一质点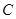从原点出发，始终沿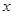轴的正方向运动，已知第1分钟内，质点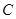运动了1个单位，之后每分钟内比上一分钟内多运动了2个单位，记第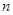分钟内质点运动了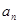个单位，此时质点的位置为．

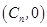（Ⅰ）求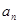、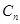的表达式；

（Ⅱ）当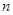为何值时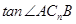，取得最大，最大值为多少？

 

Answer 1

【答案】

（Ⅰ）．

（Ⅱ）时，最大，最大值为．

【解析】(I)解本小题关键是由条件可知，第分钟内，质点运动了个单位，C_n就表示数列{a_n}的前n项和.

(II)根据,可用n表示出,然后采用函数求最值的方法求其最大值.

解：（Ⅰ）由条件可知，第分钟内，质点运动了个单位，

……2分       所以．………… 4分

（Ⅱ）,…………6分

．………… 8分

…………10分

当且仅当，即时，等号成立．………… 11分

∴时，最大，最大值为．………… 12分