题目内容
如图，一个空间几何体的正视图，侧视图，府视图均为全等的等腰直角三角形；如直角三角形的直角边的长为1，那么这个几何体的体积为（ ）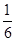
B.
C.
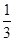D.1
A
解析考点：由三视图求面积、体积．
分析：由三视图及题设条件知，此几何体为一个三棱锥，其高已知，底面是长度为1的等腰直角三角形，故先求出底面积，再由体积公式求解其体积即可．
解：由题设条件，此几何几何体为一个三棱锥，其高已知为2，底面是长度为2的直角三角形，
底面积是
×1×1=
其体积是
××1=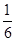
故选A
练习册系列答案
相关题目
已知一个长方体的同一顶点处的三条棱长分别为1，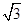
，2，则其外接球的表面积为
A． | B． | C． | D． |
平面A1B1C1，正视图是边长为2的正方形，俯视图为一个等边三角形，该三棱柱的左视图的面积为 （ ）
设图是某几何体的三视图，则该几何体的体积为（ ）
A． | B． |
C． | D． |
如图，AA1是长方体的一条棱，这个长方体中与AA1异面的棱的条数是
| A．6 | B．4 | C． 5 | D．8 |
如图，下列四个几何体中，它们的三视图(正视图、侧视图、俯视图)有且仅有两个相同的是( )
| A．(1)(2) | B．(1)(3) | C．(2)(3) | D．(1)(4) |
容器中水面的高度
随时间
变化的可能图象是（ ）
在平面上，若两个正三角形的边长比
为1:2.则它们的面积之比为1:4.类似地，在空间中，若两个正四面体的棱长比为1:2，则它们
的体积比为（ ）
| A．1:2 | B．1:4 | C．1:6 | D．1:8 |
4.关于斜二侧画法，下列说法正确的是（ ）
| A．三角形的直观图可能是一条线段 |
| B．平行四边形的直观图一定是平行四边形 |
| C．正方形的直观图是正方形 |
| D．菱形的直观图是菱形 |