题目内容
20.已知椭圆方程为$\frac{{x}^{2}}{8}+\frac{{y}^{2}}{2}=1$,过椭圆上一点P(2,1)作切线交y轴于N,过P的另一条直线交y轴于M,若△PMN是以MN为底边的等腰三角形,则直线PM的方程为( )| A. | y=$\frac{3}{2}x-2$ | B. | y=$\frac{1}{2}x$ | C. | y=-2x+5 | D. | y=$\frac{2}{3}x-\frac{1}{3}$ |
分析 如图所示,设点P(2,1)作切线PN,设切线方程为:y-1=k(x-2),与椭圆方程联立可得(1+4k2)x2+8k(1-2k)x+4(1-2k)2-8=0,令△=0,解得k=-$\frac{1}{2}$.可得切线PN的方程为:y=-$\frac{1}{2}$x+2,可得N坐标,即可得出M的坐标,可得直线PM的方程.
解答 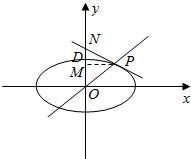 解:如图所示,
解:如图所示,
设点P(2,1)作切线PN,设切线方程为:y-1=k(x-2),
联立$\left\{\begin{array}{l}{y-1=k(x-2)}\\{{x}^{2}+4{y}^{2}=8}\end{array}\right.$,化为(1+4k2)x2+8k(1-2k)x+4(1-2k)2-8=0,
∵△=64k2(1-2k)2-4(1+4k2)[4(1-2k)2-8]=0,
化为(2k+1)2=0,
解得k=-$\frac{1}{2}$.
∴切线PN的方程为:y=-$\frac{1}{2}$x+2,
令x=0,解得y=2,
∴N(0,2).
过点P作PD⊥y轴,垂足为D(0,1).
∵△PMN是以MN为底边的等腰三角形,
∴N(0,0),即与原点O重合.
∴直线PM的方程为:$y=\frac{1}{2}x$,
故选:B.
点评 本题考查了椭圆的标准方程及其性质、椭圆的切线的性质、等腰三角形的性质、直线的方程,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
8.双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左右焦点分别为F1、F2,已知线段F1F2被点(b,0)分成3:1的两段,则此双曲线的离心率为( )
| A. | $\frac{\sqrt{3}}{2}$ | B. | $\frac{2\sqrt{3}}{3}$ | C. | $\frac{\sqrt{5}}{2}$ | D. | $\frac{2\sqrt{5}}{5}$ |
9.若x,y>0,且x+2y=1,则(x+$\frac{1}{x}$)(y+$\frac{1}{4y}$)的最小值是( )
| A. | $\frac{25}{2}$ | B. | $\frac{25}{4}$ | C. | $\frac{25}{8}$ | D. | $\frac{25}{16}$ |