题目内容
（2013•延庆县一模）已知直线l1：ax+（a+1）y+1=0，l2：x+ay+2=0，则“a=-2”是“l1⊥l2”（ ）
分析：利用a=-2判断两条直线是否垂直，然后利用两条在的垂直求出a是的值，利用充要条件判断即可．
解答：解：因为直线l1：ax+（a+1）y+1=0，l2：x+ay+2=0，
当“a=-2”时，直线l1：-2x-y+1=0，l2：x-2y+2=0，满足k1•k2=-1，∴“l1⊥l2”．
如果l1⊥l2，所以a•1+（a+1）a=0，解答a=-2或a=0，
所以直线l1：ax+（a+1）y+1=0，l2：x+ay+2=0，则“a=-2”是“l1⊥l2”充分不必要条件．
故选A．
当“a=-2”时，直线l1：-2x-y+1=0，l2：x-2y+2=0，满足k1•k2=-1，∴“l1⊥l2”．
如果l1⊥l2，所以a•1+（a+1）a=0，解答a=-2或a=0，
所以直线l1：ax+（a+1）y+1=0，l2：x+ay+2=0，则“a=-2”是“l1⊥l2”充分不必要条件．
故选A．
点评：本题考查两条直线的位置关系，充要条件的判断方法的应用，考查计算能力．
练习册系列答案
提分百分百检测卷单元期末测试卷系列答案
小学期末标准试卷系列答案
相关题目
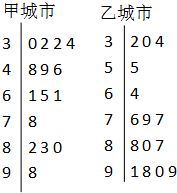（2013•延庆县一模）空气质量指数PM2.5（单位：μg/m3）表示每立方米空气中可入肺颗粒物的含量，这个值越高，就代表空气污染越严重：
（2013•延庆县一模）如图，四棱锥P-ABCD的底面ABCD为菱形，∠ABC=60°，PA⊥底面ABCD，PA=AB=2，E为PA的中点．