题目内容
已知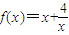 ,当x∈[1,3]时的值域为[n,m],则m-n的值是( )
,当x∈[1,3]时的值域为[n,m],则m-n的值是( )A.

B.

C.1
D.

【答案】分析:先对函数求导,可得f′(x)=1- ,判断其在[1,3]上的符号可得f(x)的单调性,进而可得最小值即n的值,比较端点值的大小,可得最大值即m;进而可得答案.
,判断其在[1,3]上的符号可得f(x)的单调性,进而可得最小值即n的值,比较端点值的大小,可得最大值即m;进而可得答案.
解答:解:f(x)=x+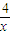 ,则f′(x)=1-
,则f′(x)=1-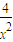 ,
,
易得在[1,2]上,f′(x)<0,则f(x)是减函数,在[2,3]上,f′(x)>0,则f(x)是增函数,
则f(x)在[1,3]上最小值为f(2)=4,即n=4;
且f(1)=5,f(3)=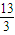 ,有f(1)>f(3),
,有f(1)>f(3),
则f(x)在[1,3]上最大值为f(1)=5,即m=4;
m-n=5-4=1;
故选C.
点评:本题考查利用导数求函数在闭区间的最值,解题的关键在于正确求出导函数,并判断导函数在区间上的符号.
 ,判断其在[1,3]上的符号可得f(x)的单调性,进而可得最小值即n的值,比较端点值的大小,可得最大值即m;进而可得答案.
,判断其在[1,3]上的符号可得f(x)的单调性,进而可得最小值即n的值,比较端点值的大小,可得最大值即m;进而可得答案.解答:解:f(x)=x+
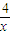 ,则f′(x)=1-
,则f′(x)=1-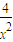 ,
,易得在[1,2]上,f′(x)<0,则f(x)是减函数,在[2,3]上,f′(x)>0,则f(x)是增函数,
则f(x)在[1,3]上最小值为f(2)=4,即n=4;
且f(1)=5,f(3)=
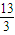 ,有f(1)>f(3),
,有f(1)>f(3),则f(x)在[1,3]上最大值为f(1)=5,即m=4;
m-n=5-4=1;
故选C.
点评:本题考查利用导数求函数在闭区间的最值,解题的关键在于正确求出导函数,并判断导函数在区间上的符号.

练习册系列答案
 高效智能课时作业系列答案
高效智能课时作业系列答案 捷径训练检测卷系列答案
捷径训练检测卷系列答案
相关题目
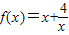 ,当x∈[1,3]时的值域为[n,m],则m-n的值是( )
,当x∈[1,3]时的值域为[n,m],则m-n的值是( )


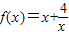 ,当x∈[1,3]时的值域为[n,m],则m-n的值是( )
,当x∈[1,3]时的值域为[n,m],则m-n的值是( )


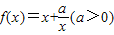 ,当x∈[1,3]时,f(x)的值域为A,且A⊆[n,m](n<m).
,当x∈[1,3]时,f(x)的值域为A,且A⊆[n,m](n<m).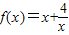 ,当x∈[1,3]时的值域为[n,m],则m-n的值是( )
,当x∈[1,3]时的值域为[n,m],则m-n的值是( )

