题目内容
已知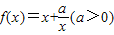 ,当x∈[1,3]时,f(x)的值域为A,且A⊆[n,m](n<m).
,当x∈[1,3]时,f(x)的值域为A,且A⊆[n,m](n<m).(1)若a=1,求m-n的最小值;
(2)若m=16,n=8,求a的值;
(3)若m-n≤1,且A=[n,m],求a的取值范围.
【答案】分析:(Ⅰ)利用函数的单调性可得f(x)∈[f(1),f(3)],由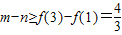 ,求得m-n的最小值.
,求得m-n的最小值.
(Ⅱ)由题意可得,当m=16时,a≤16x-x2恒成立,a≤(-x2+16x)min =15.当n=8时,a≥8x-x2恒成立,a≥(-x2+8x)max =15,由此求得a的值.
(3)根据 m-n≤1,且A=[n,m],分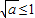 、
、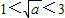 和
和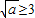 三种情况,分别求出a的取值范围,再取并集,即得所求.
三种情况,分别求出a的取值范围,再取并集,即得所求.
解答:解:(Ⅰ)∵a=1,∴f(x)在区间[1,3]上单调递增,∴f(x)∈[f(1),f(3)],…(3分)
∴当x∈[1,3]时,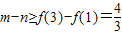 ,即m-n的最小值是
,即m-n的最小值是 .…(5分)
.…(5分)
(Ⅱ)由题意可得,当m=16时,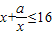 恒成立,即当x∈[1,3]时,a≤16x-x2恒成立,
恒成立,即当x∈[1,3]时,a≤16x-x2恒成立,
∴a≤(-x2+16x)min =15.…(7分)
当n=8时,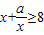 恒成立,即当x∈[1,3]时,a≥8x-x2恒成立,∴a≥(-x2+8x)max =15.…(9分)
恒成立,即当x∈[1,3]时,a≥8x-x2恒成立,∴a≥(-x2+8x)max =15.…(9分)
综上可得:a=15.…(10分)
(Ⅲ)①若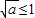 ,即0<a≤1时,
,即0<a≤1时,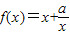 在[1,3]单调递增,
在[1,3]单调递增,
∴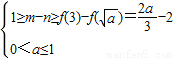 ,a无解.…(11分)
,a无解.…(11分)
②当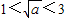 ,即1<a<9时,
,即1<a<9时,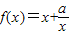 在
在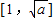 递减,在
递减,在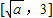 递增,
递增,
∴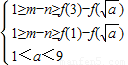 ,∴
,∴ ,
,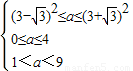 ,
,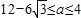 .…(13分)
.…(13分)
③当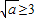 ,即a≥9时,函数f(x)在区间[1,3]上单调递减,
,即a≥9时,函数f(x)在区间[1,3]上单调递减,
∴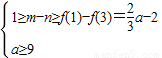 ,a无解;…(14分),
,a无解;…(14分),
综上可得: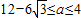 .…(16分)
.…(16分)
点评:本题主要考查利用函数的单调性求函数的值域,体现了分类讨论的数学思想,属于中档题.
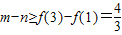 ,求得m-n的最小值.
,求得m-n的最小值.(Ⅱ)由题意可得,当m=16时,a≤16x-x2恒成立,a≤(-x2+16x)min =15.当n=8时,a≥8x-x2恒成立,a≥(-x2+8x)max =15,由此求得a的值.
(3)根据 m-n≤1,且A=[n,m],分
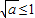 、
、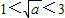 和
和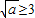 三种情况,分别求出a的取值范围,再取并集,即得所求.
三种情况,分别求出a的取值范围,再取并集,即得所求.解答:解:(Ⅰ)∵a=1,∴f(x)在区间[1,3]上单调递增,∴f(x)∈[f(1),f(3)],…(3分)
∴当x∈[1,3]时,
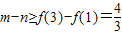 ,即m-n的最小值是
,即m-n的最小值是 .…(5分)
.…(5分)(Ⅱ)由题意可得,当m=16时,
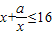 恒成立,即当x∈[1,3]时,a≤16x-x2恒成立,
恒成立,即当x∈[1,3]时,a≤16x-x2恒成立,∴a≤(-x2+16x)min =15.…(7分)
当n=8时,
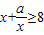 恒成立,即当x∈[1,3]时,a≥8x-x2恒成立,∴a≥(-x2+8x)max =15.…(9分)
恒成立,即当x∈[1,3]时,a≥8x-x2恒成立,∴a≥(-x2+8x)max =15.…(9分)综上可得:a=15.…(10分)
(Ⅲ)①若
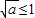 ,即0<a≤1时,
,即0<a≤1时,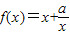 在[1,3]单调递增,
在[1,3]单调递增,∴
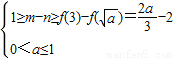 ,a无解.…(11分)
,a无解.…(11分)②当
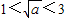 ,即1<a<9时,
,即1<a<9时,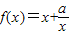 在
在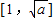 递减,在
递减,在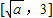 递增,
递增,∴
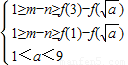 ,∴
,∴ ,
,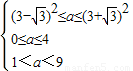 ,
,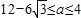 .…(13分)
.…(13分)③当
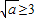 ,即a≥9时,函数f(x)在区间[1,3]上单调递减,
,即a≥9时,函数f(x)在区间[1,3]上单调递减,∴
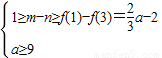 ,a无解;…(14分),
,a无解;…(14分),综上可得:
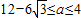 .…(16分)
.…(16分)点评:本题主要考查利用函数的单调性求函数的值域,体现了分类讨论的数学思想,属于中档题.

练习册系列答案
 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案
相关题目
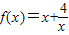 ,当x∈[1,3]时的值域为[n,m],则m-n的值是( )
,当x∈[1,3]时的值域为[n,m],则m-n的值是( )


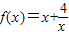 ,当x∈[1,3]时的值域为[n,m],则m-n的值是( )
,当x∈[1,3]时的值域为[n,m],则m-n的值是( )


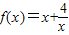 ,当x∈[1,3]时的值域为[n,m],则m-n的值是( )
,当x∈[1,3]时的值域为[n,m],则m-n的值是( )


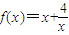 ,当x∈[1,3]时的值域为[n,m],则m-n的值是( )
,当x∈[1,3]时的值域为[n,m],则m-n的值是( )

