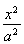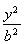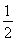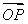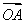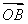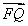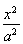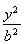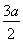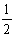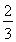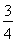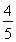题目内容
椭圆E: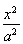 +
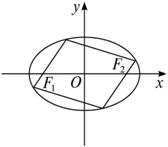
+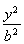 =1(a>b>0)的左、右焦点分别为F1,F2,焦距为2,过F1作垂直于椭圆长轴的弦PQ,|PQ|为3.
=1(a>b>0)的左、右焦点分别为F1,F2,焦距为2,过F1作垂直于椭圆长轴的弦PQ,|PQ|为3.
(1)求椭圆E的方程;
(2)若过F1的直线l交椭圆于A,B两点,判断是否存在直线l使得∠AF2B为钝角,若存在,求出l的斜率k的取值范围.
【答案】
(1) 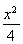 +
+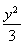 =1 (2)存在,斜率k的取值范围为-
=1 (2)存在,斜率k的取值范围为-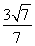 <k<
<k<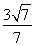
【解析】
解:(1)依题意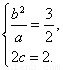
解得a2=4,b2=3,
∴椭圆的方程为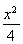 +
+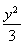 =1.
=1.
(2)①当过F1的直线AB的斜率不存在时,
不妨取A(-1,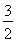 ),B(-1,-
),B(-1,-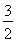 )
)
则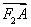 ·
·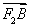 =
=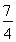 ,显然∠AF2B不为钝角.
,显然∠AF2B不为钝角.
②直线l的斜率为k,l方程为y=k(x+1),
由
消去y,整理得(3+4k2)x2+8k2x+4k2-12=0.
∵直线l与椭圆交于两点,
∴Δ=(8k2)2-4(3+4k2)(4k2-12)=4×36(k2+1)>0.
设A(x1,y1),B(x2,y2),
则x1+x2=-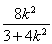 ,x1·x2=
,x1·x2=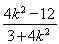 .
.
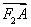 =(x1-1,y1),
=(x1-1,y1),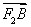 =(x2-1,y2).
=(x2-1,y2).
∵∠AF2B为钝角,
∴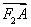 ·
·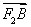 <0.
<0.
即(x1-1)(x2-1)+y1y2<0,
整理得(k2+1)x1x2+(k2-1)(x1+x2)+k2+1<0.
即(k2+1)·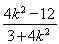 -(k2-1)·
-(k2-1)·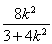 +k2+1<0,
+k2+1<0,
整理得7k2<9,
解得-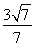 <k<
<k<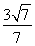 .
.
∴存在满足条件的直线l,
其斜率k的取值范围为-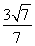 <k<
<k<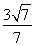 .
.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
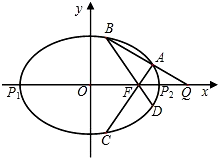 (2013•宁波二模)如图,已知椭圆E:
(2013•宁波二模)如图,已知椭圆E: