题目内容
已知点P(-3,0),点A在y轴上,点Q在x轴非负半轴上,点M在直线AQ上,满足 ·
· =0,
=0, =-
=-
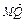 .
.
(1)当点A在y轴上移动时,求动点M的轨迹C的方程;
(2)设轨迹C的准线为l,焦点为F,过F作直线m交轨迹C于G,H两点,过点G作平行于轨迹C的对称轴的直线n,且n∩l=E,试问点E,O,H(O为坐标原点)是否在同一条直线上?并说明理由.
 ·
· =0,
=0, =-
=-
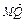 .
.(1)当点A在y轴上移动时,求动点M的轨迹C的方程;
(2)设轨迹C的准线为l,焦点为F,过F作直线m交轨迹C于G,H两点,过点G作平行于轨迹C的对称轴的直线n,且n∩l=E,试问点E,O,H(O为坐标原点)是否在同一条直线上?并说明理由.
(1)M点的轨迹方程为y2=4x,(2)O,E,H三点共线
(1)设M(x,y)为轨迹上任意一点,
A(0,b),Q(a,0)(a≥0),
则 =(x,y-b),
=(x,y-b),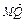 ="(a-x,-y),"
="(a-x,-y),"
∵ =-
=-
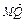 ,
,
∴(x,y-b)=- (a-x,-y),
(a-x,-y),
∴ ,从而
,从而 .
.
∴A ,且
,且 =
= ,
,  =
= .
.
∵ ·
· =0,
=0,
∴ ·
· =0,即3x-
=0,即3x- y2=0,
y2=0,
∴y2=4x,故M点的轨迹方程为y2=4x.
(2)轨迹C的焦点为F(1,0),准线为l:x=-1,对称轴为x轴.设直线m的方程为y=k(x-1)(k≠0),
由
 ky2-4y-4k=0,
ky2-4y-4k=0,
设G(x1,y1),H(x2,y2),
则由根与系数的关系得,y1y2=-4,
又由已知 =(-1,y1),
=(-1,y1), =
= ,
,
∴(-1)×y2-y1× =-y2-
=-y2- ·y2=-y2+y2=0,
·y2=-y2+y2=0,
∴ ∥
∥ ,故O,E,H三点共线.
,故O,E,H三点共线.
A(0,b),Q(a,0)(a≥0),
则
 =(x,y-b),
=(x,y-b),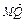 ="(a-x,-y),"
="(a-x,-y)," ∵
 =-
=-
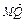 ,
,∴(x,y-b)=-
 (a-x,-y),
(a-x,-y),∴
 ,从而
,从而 .
.∴A
 ,且
,且 =
= ,
,  =
= .
.∵
 ·
· =0,
=0,∴
 ·
· =0,即3x-
=0,即3x- y2=0,
y2=0,∴y2=4x,故M点的轨迹方程为y2=4x.
(2)轨迹C的焦点为F(1,0),准线为l:x=-1,对称轴为x轴.设直线m的方程为y=k(x-1)(k≠0),
由

 ky2-4y-4k=0,
ky2-4y-4k=0,设G(x1,y1),H(x2,y2),
则由根与系数的关系得,y1y2=-4,
又由已知
 =(-1,y1),
=(-1,y1), =
= ,
,∴(-1)×y2-y1×
 =-y2-
=-y2- ·y2=-y2+y2=0,
·y2=-y2+y2=0,∴
 ∥
∥ ,故O,E,H三点共线.
,故O,E,H三点共线.
练习册系列答案
 阶梯计算系列答案
阶梯计算系列答案
相关题目
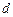 万公里时,经过地球和慧得的直线与抛物线对称轴的夹角为
万公里时,经过地球和慧得的直线与抛物线对称轴的夹角为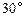 ,求此慧星运行时离地球的最近距离.
,求此慧星运行时离地球的最近距离.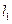 过点A,且与抛物线C 相切,直线
过点A,且与抛物线C 相切,直线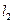 :x=a(a≠-1)交抛物线C于B,交直线
:x=a(a≠-1)交抛物线C于B,交直线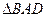 的面积为S1,求
的面积为S1,求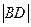 及S1的值.
及S1的值.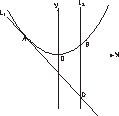
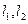 所围成的图形的面积为S2,求证S1:S2的值为与a无关的常数.
所围成的图形的面积为S2,求证S1:S2的值为与a无关的常数.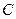 经过定点
经过定点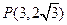 ,它的一个焦点为
,它的一个焦点为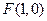 ,对应于该焦点的
,对应于该焦点的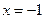 ,斜率为
,斜率为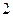 的直线
的直线 交圆锥曲线
交圆锥曲线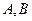 两点,且
两点,且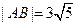 ,
,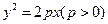 的焦点作倾斜角为
的焦点作倾斜角为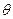 的直线
的直线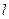 ,设
,设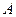 ,
,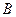 两点,求
两点,求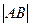 .
.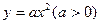 的焦点F作一直线交抛物线于P、Q两点,若线段DF与FQ的长分别是p,q,则
的焦点F作一直线交抛物线于P、Q两点,若线段DF与FQ的长分别是p,q,则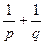 等于______________。
等于______________。