题目内容
已知△ABC的内角A，B及其对边a，b满足a+b=acotA+bcotB，求内角C．
解：由已知及正弦定理，有sinA+sinB=sinA•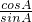
+sinB•
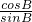=cosA+cosB，
∴sinA-cosA=cosB-sinB
∴sin（A-
）=sin（B+
），
∵0＜A＜π，0＜B＜π
∴-＜A-＜＜B+＜
∴A-+B+=π，
∴A+B=
，C=π-（A+B）=
分析：先利用正弦定理题设等式中的边转化角的正弦，化简整理求得sin（A-）=sin（B+），，进而根据A，B的范围，求得A-和B+的关系，进而求得A+B=，则C的值可求．
点评：本题主要考查了正弦定理的应用．解题过程中关键是利用了正弦定理把边的问题转化为角的问题．
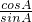+sinB•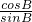=cosA+cosB，∴sinA-cosA=cosB-sinB
∴sin（A-
）=sin（B+），∵0＜A＜π，0＜B＜π
∴-
＜A-＜＜B+＜∴A-
+B+=π，∴A+B=
，C=π-（A+B）=分析：先利用正弦定理题设等式中的边转化角的正弦，化简整理求得sin（A-
）=sin（B+），，进而根据A，B的范围，求得A-和B+的关系，进而求得A+B=，则C的值可求．点评：本题主要考查了正弦定理的应用．解题过程中关键是利用了正弦定理把边的问题转化为角的问题．
练习册系列答案
超能学典应用题题卡系列答案
相关题目