题目内容
“
”是“函数
的最小正周期为
”的（ ）.
| A．充分必要条件 | B．充分不必要条件 |
| C．必要不充分条件 | D．既不充分又必要条件 |
B
解析试题分析：因为可化为
.所以可得是函数
最小正周期为的充分条件.由于函数的最小正周期为
,则
.所以必要性不成立.故选B.
考点：1.三角函数的恒等变形.2.充要条件的知识.
练习册系列答案
相关题目
已知命题p：“?x∈R，?m∈R，使4x＋2x·m＋1＝0”．若命题p为真命题，则实数m的取值范围是
| A．(－∞，－2] |
| B．[2,+∞) |
| C．(－∞，－2) |
| D．(2,+∞) |
已知命题p：?x0∈R，使sin x0＝
；命题q：?x∈R，都有x2＋x＋1＞0.
给出下列结论 ①命题“p∧q”是真命题； ②命题“¬p∨¬q”是假命题；
③命题“¬p∨q”是真命题； ④命题“p∨¬q”是假命题．
其中正确的是
| A．②③ |
| B．②④ |
| C．③④ |
| D．①②③ |
已知命题
“
”，命题
“
”，若命题“
” 是真命题，则实数
的取值范围是（ ）
A． | B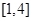． | C． | D． |
已知空间直线
不在平面
内，则“直线上有两个点到平面的距离相等”是“
”的( )．
| A．充分非必要条件 | B．必要非充分条件 | C．充要条件 | D．非充分非必要条件 |
是“甲落地站稳”,
是“乙落地站稳”,则命题“至少有一位队员落地没有站稳”可表示为（ ）
已知命题
的否定为假命题，则实数m的取值范围是（ ）
A． | B． | C．[﹣1，2] | D． |
命题“任意多面体的面至少有一个是三角形或四边形或五边形”的结论的否定形式是 ( )
| A．任意多面体没有一个是三角形或四边形或五边形的面 |
| B．任意多面体没有一个是三角形的面 |
| C．任意多面体没有一个是四边形的面 |
| D．任意多面体没有一个是五边形的面 |