题目内容
已知f（x）=sinx+acosx的图象的一条对称轴是
，则g（x）=asinx+cosx的初相是（ ）A．
B．
C．
D．
【答案】分析：先利用函数的对称性，采用赋值法列方程解得a的值，再利用两角和的正弦公式将函数g（x）化为y=Asin（ωx+φ）型函数，从而确定其初相φ
解答：解：∵f（x）=sinx+acosx的图象的一条对称轴是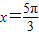
，
∴f（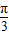
）=f（3π）
即sin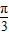
+acos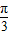
=sin3π+acos3π，解得a=-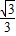
∴g（x）=-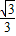
sinx+cosx=
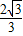（sinxcos
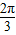+cosxsin
）=
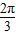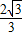sin（x+
）
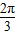∴g（x）=asinx+cosx的初相是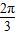
故选 D
点评：本题主要考查了三角函数的图象和性质，利用对称性和赋值法求参数值的技巧，y=Asin（ωx+φ）型函数的意义，属基础题
解答：解：∵f（x）=sinx+acosx的图象的一条对称轴是
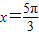，∴f（
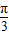）=f（3π）即sin
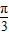+acos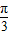=sin3π+acos3π，解得a=-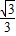∴g（x）=-
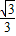sinx+cosx=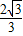（sinxcos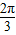+cosxsin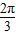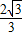）=sin（x+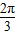）∴g（x）=asinx+cosx的初相是
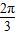
故选 D
点评：本题主要考查了三角函数的图象和性质，利用对称性和赋值法求参数值的技巧，y=Asin（ωx+φ）型函数的意义，属基础题
练习册系列答案
名校课堂系列答案
相关题目
已知f（x）=sin（x+
），g（x）=cos（x-
），则f（x）的图象（ ）
| π |
| 2 |
| π |
| 2 |
| A、与g（x）的图象相同 | ||
| B、与g（x）的图象关于y轴对称 | ||
C、向左平移
| ||
D、向右平移
|