题目内容
【题目】
如图,平行四边形![]() 中,
中,![]() ,
,![]() 将
将![]() 沿
沿![]() 折起到
折起到![]() 的位置,使平面
的位置,使平面![]() 平面
平面![]() .
.
(Ⅰ)求证:![]() ;
;
(Ⅱ)求三棱锥![]() 的侧面积.
的侧面积.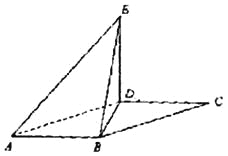
【答案】(Ⅰ)证明见解析.
(Ⅱ)![]()
【解析】
试题(1)在△ABD 中,∵AB=2,AD=4,∠DAB=60°,
∴BD=![]() .
.
∴AB2+BD2=AD2,∴AB⊥BD.
又∵平面EBD⊥平面ABD,
平面EBD∩平面ABD=BD,AB![]() 平面ABD,
平面ABD,
∴AB⊥平面EBD. 又∵DE![]() 平面EBC,∴AB⊥DE. ……5分
平面EBC,∴AB⊥DE. ……5分
(2)由(1)知AB⊥BD.
∵CD∥AB ∴CD⊥BD,从而DE⊥BD
在Rt△DBE中, ∵DB=2![]() ,DE=DC=AB=2,
,DE=DC=AB=2,
∴S△DBE=![]() .……7分
.……7分
又∵AB⊥平面EBD,BE![]() 平面EBD,∴AB⊥BE.
平面EBD,∴AB⊥BE.
∵BE=BC=AD=4,S△ABE=![]() AB·BE=4……9分
AB·BE=4……9分
∵DE⊥BD,平面EBD⊥平面ABD,∴ED⊥平面ABD,
而AD![]() 平面ABD,∴ED⊥AD,∴S△ADE=
平面ABD,∴ED⊥AD,∴S△ADE=![]() AD·DE="4." ……11分
AD·DE="4." ……11分
综上,三棱锥E—ABD的侧面积S=8+2![]() . ……12分
. ……12分

练习册系列答案
相关题目