题目内容
已知点A(-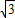 ,0)和B(
,0)和B(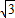 ,0),动点C到A、B两点的距离之差的绝对值为2.
,0),动点C到A、B两点的距离之差的绝对值为2.求:
(1)点C的轨迹方程;
(2)设动点C的轨迹与直线y=x-2交于D、E两点,求线段DE的长.
【答案】分析:(1)由点A(- ,0)和B(
,0)和B( ,0),动点C到A、B两点的距离之差的绝对值为2.知C的轨迹是以A(-
,0),动点C到A、B两点的距离之差的绝对值为2.知C的轨迹是以A(-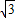 ,0)和B(
,0)和B(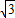 ,0)为焦点的双曲线,由此能求出C的轨迹方程.
,0)为焦点的双曲线,由此能求出C的轨迹方程.
(2)C的轨迹方程是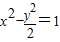 ,联立
,联立 ,得x2+4x-6=0,由此能求出线段DE的长.
,得x2+4x-6=0,由此能求出线段DE的长.
解答:解:(1)∵点A(-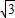 ,0)和B(
,0)和B( ,0),
,0),
动点C到A、B两点的距离之差的绝对值为2.
|AB|=2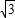 >2,
>2,
∴C的轨迹方程是以A(-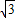 ,0)和B(
,0)和B(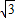 ,0)为焦点的双曲线,
,0)为焦点的双曲线,
且a=1,c= ,
,
∴C的轨迹方程是 .
.
(2)∵C的轨迹方程是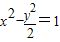 ,
,
∴联立 ,得x2+4x-6=0,
,得x2+4x-6=0,
设D(x1,y1)、E(x2,y2),则x1+x2=-4,x1x2=-6,
∴|DE|= =4
=4 .
.
故线段DE的长为4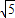 .
.
点评:本题考查点的轨迹方程的求法,考查弦长的求法.解题时要认真审题,仔细解答,注意双曲线的定义和弦长公式的合理运用.
 ,0)和B(
,0)和B( ,0),动点C到A、B两点的距离之差的绝对值为2.知C的轨迹是以A(-
,0),动点C到A、B两点的距离之差的绝对值为2.知C的轨迹是以A(-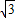 ,0)和B(
,0)和B(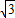 ,0)为焦点的双曲线,由此能求出C的轨迹方程.
,0)为焦点的双曲线,由此能求出C的轨迹方程.(2)C的轨迹方程是
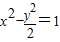 ,联立
,联立 ,得x2+4x-6=0,由此能求出线段DE的长.
,得x2+4x-6=0,由此能求出线段DE的长.解答:解:(1)∵点A(-
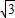 ,0)和B(
,0)和B( ,0),
,0),动点C到A、B两点的距离之差的绝对值为2.
|AB|=2
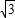 >2,
>2,∴C的轨迹方程是以A(-
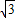 ,0)和B(
,0)和B(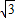 ,0)为焦点的双曲线,
,0)为焦点的双曲线,且a=1,c=
 ,
,∴C的轨迹方程是
 .
.(2)∵C的轨迹方程是
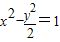 ,
,∴联立
 ,得x2+4x-6=0,
,得x2+4x-6=0,设D(x1,y1)、E(x2,y2),则x1+x2=-4,x1x2=-6,
∴|DE|=
 =4
=4 .
.故线段DE的长为4
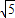 .
.点评:本题考查点的轨迹方程的求法,考查弦长的求法.解题时要认真审题,仔细解答,注意双曲线的定义和弦长公式的合理运用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 (2005•温州一模)已知点A(5,0)和⊙B:(x+5)2+y2=36,P是⊙B上的动点,直线BP与线段AP的垂直平分线交于点Q.
(2005•温州一模)已知点A(5,0)和⊙B:(x+5)2+y2=36,P是⊙B上的动点,直线BP与线段AP的垂直平分线交于点Q.