题目内容
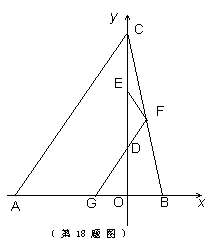
如图,![]() 的三个顶点坐标分别为
的三个顶点坐标分别为![]() ,
,![]() 分别是高
分别是高![]() 的两个三等分点,过
的两个三等分点,过![]() 作直线
作直线![]() ∥
∥![]() ,分别交
,分别交![]() 和
和![]() 于
于![]() ,连接
,连接![]() .
.
(1)求过![]() 、
、![]() 、
、![]() 三点的圆
三点的圆![]() 的方程;
的方程;
(2)在线段![]() 上是否存在点
上是否存在点![]() ,使得过点
,使得过点![]() 存在和圆M相切的直线,并且若过点
存在和圆M相切的直线,并且若过点![]() 存在两条切线时,则点
存在两条切线时,则点![]() 和两切点
和两切点![]() 组成的
组成的![]() ?若存在,求出
?若存在,求出![]() 点对应轨迹的长度;若不存在,试说明理由.
点对应轨迹的长度;若不存在,试说明理由.
 |
解(1)由已知,直线![]() 方程为:
方程为:![]()
直线![]() 方程为
方程为![]()
由![]() 可得
可得![]() ,即
,即![]() …2分
…2分
又![]() ,所以直线
,所以直线![]() 与
与![]() 的斜率之积
的斜率之积
![]() ,
,
所以![]() ,
,
所以过![]() 三点的圆
三点的圆![]() 的圆即以
的圆即以![]() 为直径的圆…………4分
为直径的圆…………4分
由![]() 知:圆心为
知:圆心为![]() ,半径
,半径![]() ,
,
所以圆![]() 的方程为
的方程为![]() ,
,
即

练习册系列答案
 一线名师提优试卷系列答案
一线名师提优试卷系列答案 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目